Jul 20 2020
Diffraction can be described as a traditional optical phenomenon that accounts for the propagation of light.
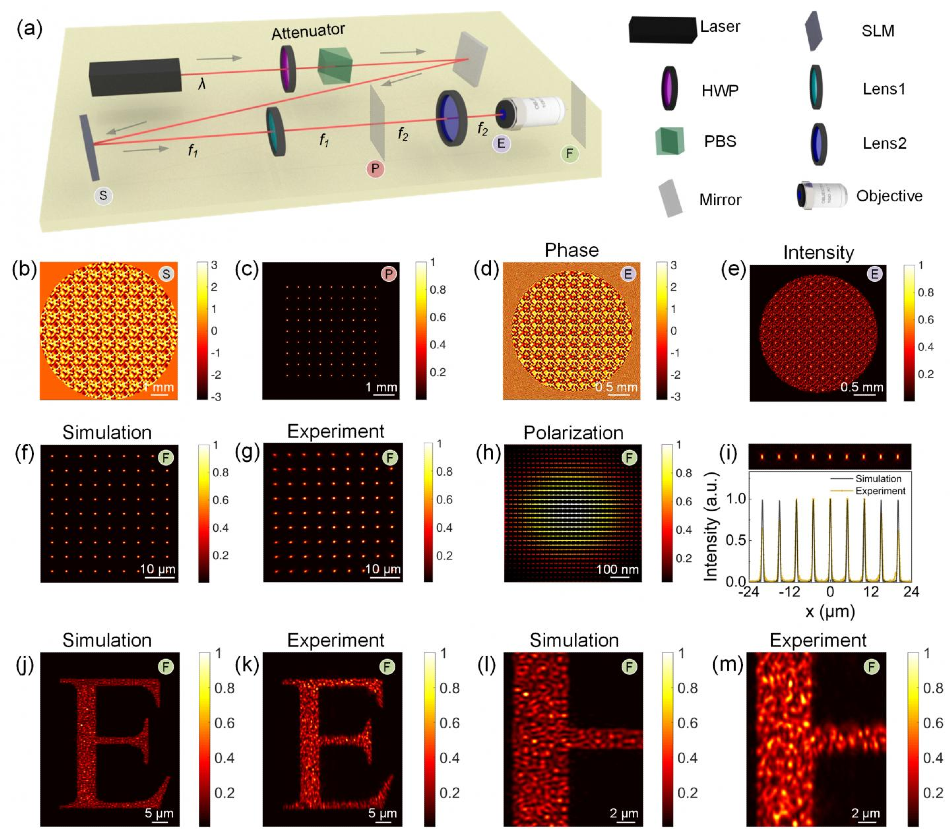(a) Sketch of the optical system. (b) CGH displayed on the SLM for the generation of a 9×9 foci array. (c) The foci array on the focal plane of Lens 1 (P plane). (d) Phase distribution and (e) intensity distribution on the entrance pupil of the objective (E plane). (f) Simulated and (g) measured multi-foci array generated on the focal plane of the objective (F plane). (h) Enlarged intensity profile of a single focal spot in the array. The arrows indicate the polarization directions. (i) Longitudinal intensity profile and corresponding line plot of the foci array. (j) Simulated and (k) measured intensity distribution on the F plane when the CGH for the generation of the pattern “E” is encoded on the SLM. (l-m) Enlarged intensity profiles of the pattern corresponding to (j) and (k) with the same sampling points as in (i). This research received funding from the National Natural Science Foundation of China, USTC Research Funds of the Double First-Class Initiative, Youth Innovation Promotion Association of the Chinese Academy of Sciences, and National Key R&D Program of China. Image Credit: Yanlei Hu, Zhongyu Wang, Xuewen Wang, Shengyun Ji, Chenchu Zhang, Jiawen Li, Wulin Zhu, Dong Wu, and Jiaru Chu.
To make a real-time prediction of light fields, it is very important to calculate the diffraction efficiently. With regard to electromagnetic (EM) waves, their diffraction can be cataloged into vector diffraction and scalar diffraction in accordance with the validation of varying approximation conditions.
While mathematical expressions for both optical diffractions have been reported convincingly for many years, fundamental advances have hardly been realized in the area of computation algorithms.
The Fast Fourier transform (FFT) technique and direct integration technique have been designed and shown to experience the limits of either poor flexibility or low efficiency. Hence, the multipurpose computation of optical diffraction in a flexible and efficient manner is extremely demanded.
After analyzing the mathematical similarities in vector diffraction and scalar diffraction, a research team has put forward an efficient full-path calculation technique. The latest study was published in the Light: Science & Applications journal.
The researchers were headed by Professor Jiawen Li and Dong Wu from CAS Key Laboratory of Mechanical Behavior and Design of Materials, Key Laboratory of Precision Scientific Instrumentation from Anhui Higher Education Institutes, Department of Precision Machinery and Precision Instrumentation, the University of Science and Technology of China, and co-workers.
Both vector diffraction and scalar diffraction are expressed through the extremely flexible Bluestein technique. One can considerably reduce the computation time to the sub-second level, which is faster by five orders of magnitude when compared to that obtained by the direct integration technique and is also faster by two orders of magnitude when compared to that obtained by the FFT technique.
Moreover, the sampling numbers and the ROIs can be randomly selected, imparting excellent flexibility to the proposed technique. Ultimately, full-path light tracing of a standard laser holographic system is demonstrated with an unparalleled computation rate, which correlates well with the experimental outcomes.
The recommended approach holds immense potential in the widespread applications of optical microscopy, manipulation, and fabrication.
Conceived by L. Bluestein and additionally generalized by L. Rabiner et al., the Bluestein technique is an elegant approach and is a potential tool in the engineer’s arsenal in the area of digital signal processing.
The Bluestein technique can execute more general Fourier transforms at random frequencies and can also increase the resolution across the entire spectrum. This provides a spectral zoom operation with random bandwidth and high resolution. The researchers have summed up the application work of the Bluestein technique in both vector and scalar diffraction computations:
We revisited and deduced the integral formulas for scalar and vector diffraction in Fourier transform forms, and then utilize the Bluestein method to completely supplant the Fourier transform in a more flexible fashion. Based on this, optical diffraction is evaluated with designated ROIs and sampling numbers.
The researchers, University of Science and Technology of China
“A few representative examples are given for both scalar and vector diffraction to demonstrate the improvement in efficiency and flexibility. Moreover, full-path light tracing of an optical holographic system is presented with unprecedented computation speed. And the results are verified by the experimental measurements,” added the researchers.
Some important adjustments are made to the conventional Bluestein method including the definition of complex starting point and additional phase shifting factor in order to cope with the realistic condition for optical calculations.
The researchers, University of Science and Technology of China
“The proposed fast and flexible method for retrieving the light field can find wide applications in the fields of optical microscopy, photolithography and optical manipulation,” forecasted the researchers.
Journal Reference:
Hu, Y., et al. (2020) Efficient full-path optical calculation of scalar and vector diffraction using the Bluestein method. Light: Science & Applications. doi.org/10.1038/s41377-020-00362-z.