Physics on the Femto- to Nanometer Scale Using High-Intensity Lasers

By Laura ThomsonJan 17 2022

The nuclear model of the atom was born in 1909 as a result of Ernest Rutherford’s α-particle backscattering experiment, which was a key step toward how the atom is visualized today—a nucleus with a diameter in femtometers surrounded by an electron cloud with a diameter in nanometers. This article looks at Fu, C. et al.'s journal published in Matter and Radiation at Extremes, looking at novel opportunities for nuclear and atomic physics on the femto- to nanometer-scale using ultra-high-intensity lasers.

Image Credit: Anusorn Nakdee/Shutterstock.com

The laws of both atomic and nuclear physics play a vital effect on the femto- to nanometer scale (FNMS). In this range, the forces involved are very simple compared to those in nuclei—beyond the nuclear surface, the powerful force’s effect rapidly diminishes, and electron motions are generally governed only by the electromagnetic force.

These puzzles may lead to a better understanding of matter’s structure and potentially to the discovery of novel physics outside of the Standard Model. The advancement of high-intensity laser technology has given the FNMS a unique approach to physics research. Narrowband lasers can be used to deduce atom and molecule structures.

Despite this, the FNMS has yet to fully harness the new prospects given by the advent of such lasers, which connect atomic and nuclear physics. This study reviews various puzzles that exist on the FNMS, and later analyzes a few theoretical techniques that can be used on the FNMS to examine many-body systems involving photons, electrons, and nuclei.

Methodology

Through a weak interaction, a free neutron decays into a proton, electron, and antineutrino. The neutron lifetime decides the speed of nucleosynthesis in the Big Bang and stars, according to nuclear astrophysics. Protons and neutrons were produced in the first few seconds after the Big Bang.

It is fascinating that a consistent experimental value for neutron lifetime has yet to be determined. Various values have been discovered by various groups using various techniques.

To determine the neutron lifetime, two types of experiments have been conducted: beam experiments, using neutron fluxes, and bottle experiments, using ultra-cold neutrons confined in containers. A more in-depth examination of the FNMS could aid in the resolution of the neutron lifetime mystery.

Another intriguing puzzle that has emerged on the FNMS is the so-called deep Dirac level (DDL). The DDL’s existence has been the topic of theoretical debate, and there are claims that the DDL is accountable for some experimentally observed phenomena, though these claims have been brought into question. It is necessary to develop new sensitive experimental detection methods.

Electron–proton elastic scattering and high-resolution spectroscopy of muonic and electronic hydrogen atoms are the two main experimental techniques for determining the proton charge radius. These various techniques produce contradictory values for the proton charge radius.

Results and Discussion

Internal conversion is a well-known process in nuclear decay. An initially free electron binds to the atom and the process is known as nuclear excitation by electron capture (NEEC) (see Figure 1).

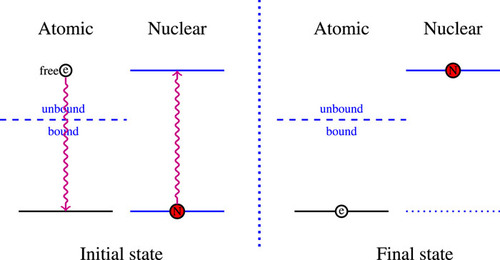
Figure 1. Atomic and nuclear states involved in a NEEC transition. Initially, the electron is unbound and the nucleus is in its ground state, whereas in the final state, the electron is bound and the nucleus is excited to a higher-energy state. Image Credit: Fu, et al., 2022

If the electron initially moves to a deeper atomic level, the process is known as nuclear excitation by electron transfer (NEET) (see Figure 2).

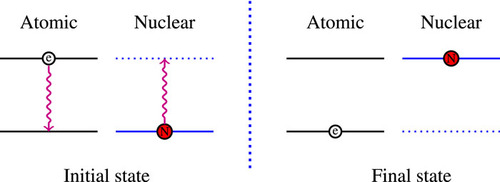
Figure 2. Atomic and nuclear states involved in a NEET transition. Initially, the electron is in a bound excited state and the nucleus is in the ground state, whereas in the final state, the electron is in a lower-energy bound state and the nucleus is in an excited state. Image Credit: Fu, et al., 2022

The electron bridge (EB) process, such as the NEET and NEEC processes, can be the dominant channel for a nuclear isomer with a resonance channel. It also has numerous advantages. Figure 3 depicts the EB process.

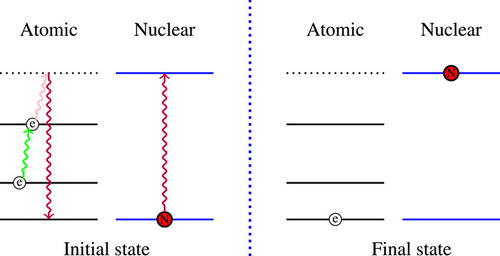
Figure 3. Atomic and nuclear states involved in an EB transition. Initially, the electron is in a bound state and the nucleus is in the ground state. When the electron absorbs a photon (pink line) or two photons (green + pink lines), it is excited to a virtual higher state. The electron may then drop to the ground state, while at the same time the nucleus is excited to a higher-energy state. Image Credit: Fu, et al., 2022

Applications

Clocks are fundamental physics devices. There would be no modern physics without precise clocks. Clocks have become increasingly precise, from ancient sundials and sandglasses to modern atomic clocks, and the search for greater precision continues. The possibility to excite nuclei to their isomer states is required for the construction of a nuclear clock.

Since lasers with suitable wavelengths and accuracy to match the isomeric energies are not available at present due to technological limitations, indirect excitation schemes such as NEEC, NEET, and EB are being explored as alternative solutions.

Physics on the FNMS does have another application: nuclear batteries. Nuclear batteries have been broadly used in deep-sea, polar exploration, and aerospace, cardiac pacemakers, and micro-electric motors, among other applications, due to their long lifetime, environmental stability, and high energy density.

High-intensity laser facilities open up new avenues for studying various physical processes occurring on the FNMS, particularly nonlinear processes.

To experimentally observe the NEEC, NEET, and EB processes in laser-induced plasmas, the nuclear isomers to be studied, as well as the intensities of the inducing lasers, must be carefully chosen. The discovery of new atomic structures may aid in the resolution of the neutron lifetime and proton charge radius puzzles.

Conclusion

Scientists looked at a few puzzles that could be linked to the FNMS. The presence of the so-called deep Dirac level, the neutron lifetime, and proton size are among them. The FNMS may be home to some yet-to-be-discovered physical processes.

They also looked at the mechanisms that link nuclear decay to atomic structures, such as the NEEC, NEET, and EB processes. The nucleus and electrons interact via the weak force for an excited nucleus with β-related decay channels, and the NEEC, NEET, and EB processes can be utilized to examine the ensuing behavior.

Current high-intensity lasers are not powerful enough to have a direct influence on nucleons in the nucleus, according to studies. They will, however, have an immediate impact on electrons bonded to a nucleus. Due to the importance of electrons in the weak interaction, high-intensity laser facilities may be crucial in solving the FNMS issues.

Journal Reference:

Fu, C., Zhang, G., Ma, Y. (2022) New opportunities for nuclear and atomic physics on the femto- to nanometer scale with ultra-high-intensity lasers. Matter and Radiation at Extremes, 7, p. 024201. Available Online: https://aip.scitation.org/doi/full/10.1063/5.0059405.

References and Further Reading

1. Schiff, L I (1968) Quantum Mechanics, 3rd ed. (McGraw-Hill Publishing Company, New York.
2. Karr, J P., et al. (2020) The proton size. Nature Reviews Physics, 2, pp. 601–614. doi.org/10.1038/s42254-020-0229-x.
3. Yue, A T., et al. (2013) Improved determination of the neutron lifetime. Physical Review Letters, 111, p. 222501. doi.org/10.1103/PhysRevLett.111.222501.
4. Wietfeldt F E & Greene, G L (2011) “Colloquium: The neutron lifetime,” Reviews of Modern Physics, 83, pp. 1173–1192. doi.org/10.1103/RevModPhys.83.1173.
5. Fu, C., et al. (2020) Feasibility Study on the Deep Dirac Levels with High-Intensity Lasers. Nuclear Physics Review, 37, pp. 377–381. doi.org/10.11804/NuclPhysRev.37.2019CNPC20.
6. Kneipp, K., et al. (1997) Single Molecule Detection Using Surface-Enhanced Raman Scattering (SERS). Physical Review Letters, 78, pp. 1667–1670. doi.org/10.1103/PhysRevLett.78.1667.
7. Harper, K. C., et al. (2019) A Laser Driven Flow Chemistry Platform for Scaling Photochemical Reactions with Visible Light. ACS Central Science, 5, pp. 109–115. doi.org/10.1021/acscentsci.8b00728.
8. Fields, B. D., et al. (2020) Big-bang nucleosynthesis after Planck. Journal of Cosmology and Astroparticle Physics, 80, p. 543. doi.org/10.1088/1475-7516/2020/03/010.
9. Paul, S (2009) “The puzzle of neutron lifetime. Nuclear Instruments and Methods in Physics Research, A 611, pp. 157–166. doi.org/10.1016/j.nima.2009.07.095.
10. Ding, W. B., et al. (2019) Neutrino emission and cooling of dark-matter-admixed neutron stars. Chinese Physics Letters, 36, p. 049701. doi.org/10.1088/0256-307X/36/4/049701.
11. Wietfeldt, F. E., et al. (2018) Measurements of the neutron lifetime,” Atoms, 6, p. 70. doi.org/10.3390/atoms6040070.
12. Goodman, B & Ignjatović S R (1997) A simpler solution of the Dirac equation in a Coulomb potential. American Journal of Physics, 65, pp. 214–221. doi.org/10.1119/1.18531.
13. Greiner, W (2000) Relativistic Quantum Mechanics, 3rd ed. (Springer-Verlag Berling Heidelberg, New York.
14. Naudts, J (2005) On the hydrino state of the relativistic hydrogen atom.
15. Phillips, J., et al. (2004) Water bath calorimetric study of excess heat generation in ‘resonant transfer’ plasmas,” Journal of Applied Physics. 96, pp. 3095–3102 doi.org/10.1063/1.1778212.
16. Mills R & Ray P (2003) Extreme ultraviolet spectroscopy of helium–hydrogen plasma. Journal of Physics D: Applied Physics. 36, p. 1535. doi.org/10.1088/0022-3727/36/13/316.
17. Va’vra, J (2013) A new way to explain the 511 keV signal from the center of the galaxy and some dark matter experiments. arXiv:1304.0833.
18. Jovićević, S., et al. (2009) Spectroscopic study of hydrogen Balmer lines in a microwave-induced discharge. Journal of Applied Physics, 105, p. 013306. doi.org/10.1063/1.3046587.
19. Rathke, A (2005) A critical analysis of the hydrino model. New Journal of Physics. 7, p. 127 doi.org/10.1088/1367-2630/7/1/127.
20. Phelps, A (2005) Comment on Water bath calorimetric study of excess heat generation in resonant transfer plasmas. Journal of Applied Physics, 96, p. 066108. doi.org/10.1063/1.1778212.
21. Dombey, N (2006) The hydrino and other unlikely states. Physics Letters A, 360, pp. 62–65. doi.org/10.1016/j.physleta.2006.07.069.
22. de Castro, A S (2007) Orthogonality criterion for banishing hydrino states from standard quantum mechanics. Physics Letters A, 369, pp. 380–383. doi.org/10.1016/j.physleta.2007.05.006.
23. Pohl, R (2010) The size of the proton. Nature, 466, pp. 213–216. https://doi.org/10.1038/nature09250.
24. Band, I. M., et al. (2002) Dirac–Fock internal conversion coefficients. Atomic Data and Nuclear Data Tables, 81, pp. 1–334. doi.org/10.1006/adnd.2002.0884.
25. Pálffy, A., et al. (2006) Theory of nuclear excitation by electron capture for heavy ions,” Physical Review A, 73, p. 012715. doi.org/10.1103/PhysRevA.73.012715.
26. Pálffy, A., et al. (2007) Quantum interference between nuclear excitation by electron capture and radiative recombination. Physical Review A, 75, p. 012709. doi.org/10.1103/physreva.75.012709.
27. Kishimoto, S., et al. (2000) Observation of nuclear excitation by electron transition in ¹⁹⁷Au with synchrotron x rays and an avalanche photodiode. Physical Review Letters. 85, pp. 1831–1834.
28. Ahmad, I., et al. (2000) Nuclear excitation by electronic transition in ¹⁸⁹Os. Physical Review C. 61, p. 051304. doi.org/10.1103/physrevc.61.051304.
29. Morel, P., et al. (2004) Nuclear excitation by electronic processes: NEEC and NEET effects. Nuclear Physics A, 746, pp. 608–612. doi.org/10.1063/1.1945195.
30. Morita, M & Otozai K (1976) Theory of nuclear excitation by electron transition (NEET) and experimental evidence in ¹⁸⁹Os and ²³⁷Np. Hyperfine Interact, 2, 418. doi.org/10.1007/bf01021198.
31. Goldanskii, V I & Namiot, V A (1976) On the excitation of isomeric nuclear levels by laser radiation through inverse internal electron conversion. Physics Letters B, 62, p. 393. doi.org/10.1016/0370-2693(76)90665-1.
32. Morel, P (2005) Nuclear excitation by electronic processes: NEEC and NEET effects. AIP Conference Proceedings.769, pp. 1085–1088. https://doi.org/10.1063/1.1945195.
33. Krutov, V A & Fomenko, V N (1968) Influence of electronic shell on gamma radiation of atomic nuclei. Annalen der Physik, 21, p. 291.
34. Bilous, P. V., et al. (2020) Electronic bridge excitation in highly charged 229Th ions,” Physical Review Letters, 124, p. 192502. doi.org/10.1103/physrevlett.124.192502.
35. McNeil, B W J & Thompson, N R (2010) X-ray free-electron lasers. Nature Photonics. 4, 814. doi.org/10.1038/nphoton.2010.239.
36. von der Wense, L & Seiferle B (2020) The ²²⁹Th isomer: Prospects for a nuclear optical clock, European Physical Journal, A 56, p. 277. doi.org/10.1140/epja/s10050-020-00263-0.
37. Cai, N. Q., et al. (2021) Populating ²²⁹Th via two-photon electronic bridge mechanism. Nuclear Science and Techniques, 32, p. 59. doi.org/10.1007/s41365-021-00900-3.
38. Brewer, S. M., et al. (2019) ²⁷Al⁺ quantum-logic clock with a systematic uncertainty below 10−18. Physical Review Letters, 123, p. 033201. doi.org/10.1103/physrevlett.123.033201.
39. Beeks, K., et al. (2021) The thorium-229 low-energy isomer and the nuclear clock. Nature Reviews Physics, 3, pp. 238–248. doi.org/10.1038/s42254-021-00286-6.
40. Marti, G E (2018) Imaging optical frequencies with 100 μHz precision and 1.1 μm resolution. Physical Review Letters, 120, p. 103201. https://doi.org/10.1103/physrevlett.120.103201.
41. Sikorsky, T (2020) Measurement of the ^229Th isomer energy with a magnetic microcalorimeter. Physical Review Letters. 125, p. 142503. doi.org/10.1103/physrevlett.125.142503.
42. Peik, E & Tamm, C (2003) Nuclear laser spectroscopy of the 3.5 eV transition in Th-229. Europhysics Letters, 61, pp. 181–186. doi.org/10.1209/epl/i2003-00210-x.
43. Campbell, C J (2012) Single-ion nuclear clock for metrology at the 19^th decimal place,” Physical Review Letters, 108, 120802. doi.org/10.1103/physrevlett.108.120802.
44. von der Wense, L (2016) Direct detection of the ^229Th nuclear clock transition. Nature 533, pp. 47–51. doi.org/10.1038/nature17669.
45. Berengut J C (2018) Resonant electronic-bridge excitation of the ²³⁵U nuclear transition in ions with chaotic spectra. Physical Review Letters, 121, p. 253002. https://doi.org/10.1103/physrevlett.121.253002.
46. Prelas, M A (2014) A review of nuclear batteries. Progress in Nuclear Energy, 75, pp. 117–148. doi.org/10.1016/j.pnucene.2014.04.007.
47. Movahedian, Z & Tavakoli-Anbaran, H (2019) Designing a nuclear battery based on the Mo-99 radioactive source soluble in water and aqua regia in order to use in early tests. Nuclear Science and Techniques, 30, p. 40. doi.org/10.1007/s41365-019-0568-4.
48. Yoon, J W (2021) Realization of laser intensity over 10²³ W/cm². Optica, 8, pp. 630–635. doi.org/10.1364/optica.420520.
49. Wang, P., et al. (2021) Super-heavy ions acceleration driven by ultrashort laser pulses at ultrahigh intensity. Physical Reviews X, 11, p. 021049. https://doi.org/10.1103/physrevx.11.021049.
50. Hollinger, R., et al. (2020) Extreme ionization of heavy atoms in solid-density plasmas by relativistic second-harmonic laser pulses. Nature Photonics, 14, p. 607. doi.org/10.1038/s41566-020-0666-1.
51. Bulanov, S. V., et al. (2003) Light intensification towards the Schwinger limit. Physical Review Letters, 91, p. 085001. doi.org/10.1103/PhysRevLett.91.085001.
52. Zhang, X., et al. (2003) Deuteron-deuteron fusion in laser-driven counter-streaming collisionless plasmas. Physical Reviews C, 96, p. 055801. doi.org/10.1103/PhysRevC.96.055801.
53. Gunst, J., et al. (2015) Direct and secondary nuclear excitation with x-ray free-electron lasers. Physics of Plasmas, 22, p. 112706. doi.org/10.1063/1.4935294.
54. He, Y. F., et al. (2020) Calibration of CR-39 solid-state track detectors for study of laser-driven nuclear reactions. Nuclear Science and Techniques, 31, p. 42. http://dx.doi.org/10.1007/s41365-020-0749-1.
55. Foord, M. E., et al. (2004) Charge-state distribution and Doppler effect in an expanding photoionized plasma. Physics Review Letters. 93, p. 055002. doi.org/10.1103/PhysRevLett.93.055002.
56. Manz, B (1967) Doppler shift in a plasma. Journal of the Optical Society of America A, 57, pp. 1543–1550. doi.org/10.1364/JOSA.57.001543.
57. Chihara, J (2000) Interaction of photons with plasmas and liquid metals – Photoabsorption and scattering. Journal of Physics: Condensed Matter, 12, pp. 231–247. doi.org/10.1088/0953-8984/12/3/303.
58. Chen, J. M., et al. (2019) Dramatic spectral broadening of ultrafast laser pulses in molecular nitrogen ions. Chinese Physics Letters, 36, p. 104204. doi.org/10.1088/0256-307X/36/10/104204.
59. Moskovits, M (1985) Surface-enhanced spectroscopy. Reviews of Modern Physics, 57, pp. 783–826. doi.org/10.1103/revmodphys.57.783.