Mar 28 2016
In recent years, computer scientists have been investigating a range of techniques for removing reflections from digital photographs shot through glass. Some have tried to use variability in focal distance or the polarization of light; others, like those at MIT, have exploited the fact that a pane of glass produces not one but two reflections, slightly offset from each other.
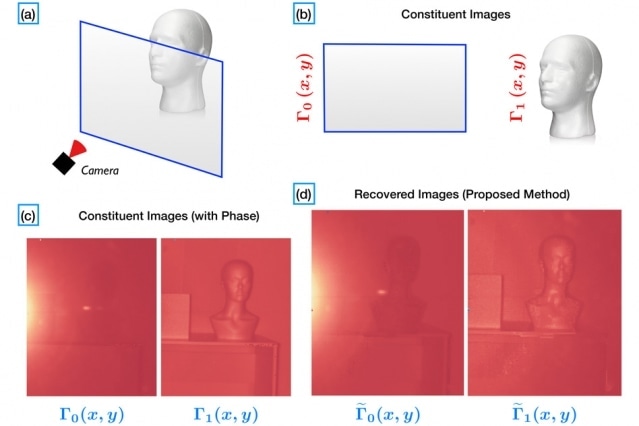Members of the MIT Media Lab’s Camera Culture Group devised a new approach to image separation in photographs. Their system fires light into a scene and gauges the differences between the arrival times of light reflected by nearby objects — such as panes of glass — and more distant objects. Courtesy of the researchers
At the Institute of Electrical and Electronics Engineers’ International Conference on Acoustics, Speech, and Signal Processing this week, members of the MIT Media Lab’s Camera Culture Group will present a fundamentally different approach to image separation. Their system fires light into a scene and gauges the differences between the arrival times of light reflected by nearby objects — such as panes of glass — and more distant objects.
In earlier projects, the Camera Culture Group has measured the arrival times of reflected light by using an ultrafast sensor called a streak camera. But the new system uses a cheap, off-the-shelf depth sensor of the type found in video game systems.
At first glance, such commercial devices would appear to be too slow to make the fine discriminations that reflection removal requires. But the MIT researchers get around that limitation with clever signal processing. Consequently, the work could also have implications for noninvasive imaging technologies such as ultrasound and terahertz imaging.
“You physically cannot make a camera that picks out multiple reflections,” says Ayush Bhandari, a PhD student in the MIT Media Lab and first author on the new paper. “That would mean that you take time slices so fast that [the camera] actually starts to operate at the speed of light, which is technically impossible. So what’s the trick? We use the Fourier transform.”
The Fourier transform, which is ubiquitous in signal processing, is a method for decomposing a signal into its constituent frequencies. If fluctuations in the intensity of the light striking a sensor, or in the voltage of an audio signal, can be represented as an erratic up-and-down squiggle, the Fourier transform redescribes them as the sum of multiple, very regular squiggles, or pure frequencies.
Phased out
Each frequency in a Fourier decomposition is characterized by two properties. One is its amplitude, or how high the crests of its waves are. This describes how much it contributes to the composite signal.
The other property is phase, which describes the offset of the wave’s troughs and crests. Two nearby frequencies may be superimposed, for instance, so that their first crests are aligned; alternatively, they might align so that the first crest of one corresponds with a trough of the other. With multiple frequencies, differences in phase alignment can yield very different composite signals.
If two light signals — one reflected from a nearby object such as a window and one from a more distant object — arrive at a light sensor at slightly different times, their Fourier decompositions will have different phases. So measuring phase provides a de facto method for measuring the signals’ time of arrival.
There’s one problem: A conventional light sensor can’t measure phase. It only measures intensity, or the energy of the light particles striking it. And in other settings, such as terahertz imaging, measuring phase as well as intensity can dramatically increase costs.
So Bhandari and his colleagues — his advisor, Ramesh Raskar, the NEC Career Development Associate Professor of Media Arts and Sciences; Aurélien Bourquard, a postdoc in MIT’s Research Laboratory of Electronics; and Shahram Izadi of Microsoft Research — instead made a few targeted measurements that allowed them to reconstruct phase information.
In collaboration with Microsoft Research, the researchers developed a special camera that emits light only of specific frequencies and gauges the intensity of the reflections. That information, coupled with knowledge of the number of different reflectors positioned between the camera and the scene of interest, enables the researchers’ algorithms to deduce the phase of the returning light and separate out signals from different depths.
Reasonable assumptions
The algorithms adapt a technique from X-ray crystallography known as phase retrieval, which earned its inventors the Nobel Prize in chemistry in 1985. “We can also exploit the fact that there should be some continuity in the intensity values in 2-D,” says Bourquard. “If your planes, for instance, are a glass window and a scene behind it, both these planes should exhibit some spatial continuity. Typically, the intensity values will not vary too fast on every separate plane. So essentially, what this phase retrieval does is use some techniques of frequency estimation, coupled with the assumption that local intensity variations within every single plane are moderate relative to the average intensity difference between these planes.”
In theory, the number of light frequencies the camera needs to emit is a function of the number of reflectors. If there is just one pane of glass between the camera and the scene of interest, the technique should require only two frequencies. If there are two panes of glass, the technique should require four frequencies.
But in practice, the light frequencies emitted by the camera are not pure, so additional measurements are required to filter out noise. In their experiments, the researchers swept through 45 frequencies to enable almost perfectly faithful image separation. That takes a full minute of exposure time, but it should be possible to make do with fewer measurements. “The interesting thing is that we have a camera that can sample in time, which was previously not used as machinery to separate imaging phenomena,” Bhandari says.
“What is remarkable about this work is the mixture of advanced mathematical concepts, such as sampling theory and phase retrieval, with real engineering achievements,” says Laurent Daudet, a professor of physics at Paris Diderot University. “I particularly enjoyed the final experiment, where the authors used a modified consumer product — the Microsoft Kinect One camera — to produce the untangled images. For this challenging problem, everyone would think that you’d need expensive, research-grade, bulky lab equipment. This is a very elegant and inspiring line of work.”