May 22 2019
A majority of people know optical lenses as transparent and curved pieces of glass or plastic, developed to focus light for cameras, spectacles, and microscopes, to name a few.
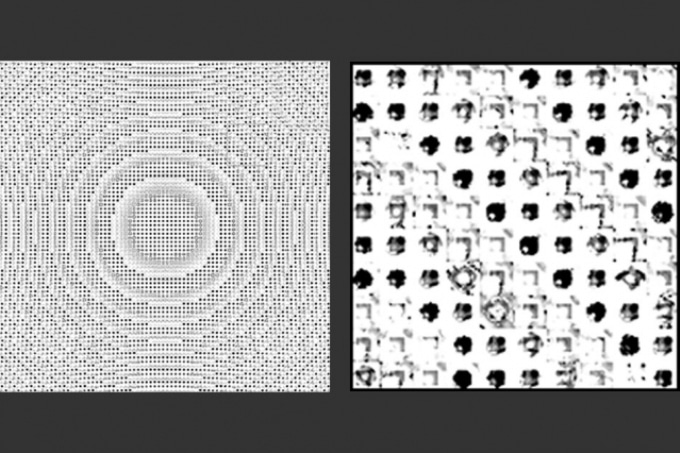 MIT mathematicians have developed a technique that quickly determines the ideal arrangement of millions of individual, microscopic features on a metasurface, to generate a flat lens that manipulates light in a specified way. The team designed a metasurface, at left, etched with millions of features. A zoomed-in image of the lens, right, shows individual features, each etched in a specific way so that, together, they produce a desired optical effect. (Image credit: Zin Lin)
MIT mathematicians have developed a technique that quickly determines the ideal arrangement of millions of individual, microscopic features on a metasurface, to generate a flat lens that manipulates light in a specified way. The team designed a metasurface, at left, etched with millions of features. A zoomed-in image of the lens, right, shows individual features, each etched in a specific way so that, together, they produce a desired optical effect. (Image credit: Zin Lin)
But for the most part, no major changes have been made to the curved shape of a lens ever since its invention several centuries ago.
However, in the past 10 years, engineers have developed flat and extremity thin materials known as “metasurfaces” that is capable of performing tricks of light much beyond the concept of what conventional curved lenses can do. On these metasurfaces, engineers etch separate features, which are hundreds of times smaller than the thickness of a single strand of human hair, to produce patterns that allow the surface as a whole to distribute light in an extremely accurate manner. Conversely, the difficulty lies in knowing the exact pattern required to create a preferred optical effect.
Now, mathematicians at MIT have developed a solution to overcome this challenge. In a study recently reported in Optics Express, a research team has described a novel computational method that rapidly establishes the perfect arrangement and makeup of a countless number of separate, tiny features on a metasurface, to produce a flat lens that controls light in a specified manner.
Studies performed in the past dealt with this problem by restricting the potential patterns to combinations of pre-established shapes, for example, spherical holes that have varied radii. However, this method merely examines a small fraction of the patterns that can possibly be created.
This is the first method to successfully design fully random patterns for large-scale optical metasurfaces that measure roughly 1 cm2, which is quite a huge area, given that each separate feature is not more than 20 nm wide. According to Steven Johnson, professor of mathematics at MIT, the new computational method can rapidly map out patterns for a series of preferred optical effects.
Say you want a lens that works well for several different colors, or you want to take light and instead of focusing it to a spot, make a beam or some sort of hologram or optical trap. You can tell us what you want to do, and this technique can come up with the pattern that you should make.
Steven Johnson, Professor, Applied Mathematics and Physics, Department of Mathematics, MIT
Johnson’s co-authors on the paper are lead author Raphaël Pestourie, Zin Lin, and Victor Liu.
Pixel-by-pixel
One metasurface is usually split into very small, nanometer-sized pixels, and each pixel can be left untouched or etched. The etched pixels can be arranged together to create any number of varied patterns.
So far, scientists have devised computer programs to look for any potential pixel pattern for tiny optical devices that measure tens of micrometers across. Precise and tiny structures like these can be used for, for example, capturing and directing light in an extremely small laser. The programs that establish the precise patterns of these tiny devices are able to do so by solving Maxwell’s equations—a series of important equations that elucidate the phenomenon of light scattering—predicated on each single pixel in a device and subsequently adjusting the pattern, pixel by pixel, until the required optical effect is produced by the structure.
However, for large-scale surfaces that measure centimeters or millimeters across, this pixel-by-pixel simulation work becomes almost impossible, says Johnson. This means a computer would have to work with a relatively larger surface region, with orders of magnitude more pixels, and it would also need to run numerous simulations of several potential pixel arrangements to ultimately reach an optimal pattern.
You have to simulate on a scale big enough to capture the whole structure, but small enough to capture fine details. The combination is really a huge computational problem if you attack it directly. If you threw the biggest supercomputer on Earth at it, and you had a lot of time, you could maybe simulate one of these patterns. But it would be a tour de force.
Steven Johnson, Professor, Applied Mathematics and Physics, Department of Mathematics, MIT
An uphill search
Now, Johnson’s group has developed a shortcut method that replicates the required pattern of pixels for large-scale optical metasurfaces in a more efficient manner. Rather than solving Maxwell’s equations for each tiny, nanometer-sized pixel in a square centimeter of material, the team solved those equations for pixel “patches.”
Then, the computer simulation developed by the researchers begins with a square centimeter of nanometer-sized and arbitrarily etched pixels. The surface was divided into groups of patches, or pixels, and then Maxwell’s equations were used for predicting how light is scattered by each patch. Subsequently, the researchers identified a method to roughly “stitch” the patch solutions together. This was done to find out how light is able to scatter across the whole, arbitrarily etched surface.
Based on this starting pattern, the investigators later modified a mathematical method called topology optimization, to fundamentally tune the pattern of individual patches over a number of iterations, until the last topology, or overall surface, scatters light in a required manner.
Johnson compares this technique to trying to find one’s way up a hill, blindfolded. A desired optical effect can be produced if every pixel in a patch has an optimal etched pattern that should be achieved and one that could be assumed to be metaphorical as a peak. Locating this peak, for each pixel in a patch, is believed to be a topology optimization challenge.
“For each simulation, we’re finding which way to tweak each pixel,” stated Johnson. “You then have a new structure which you can resimulate, and you keep doing this process, each time going uphill until you reach a peak, or optimized pattern.”
The method developed by the researchers has the potential to detect an optimal pattern in just a span of few hours, as opposed to conventional pixel-by-pixel methods which upon applying used directly to large optical metasurfaces would be almost inflexible.
With the help of their method, the scientists rapidly created optical patterns for a number of lenses, or “metadevices,” with different optical characteristics, including a solar concentrator that captures incoming light from any kind of direction and then directs it to a single point and an achromatic lens. The achromatic lens, in turn, scatters light of different colors, or wavelengths, to the same point, with the same focus.
If you have a lens in a camera, if it’s focused on you, it should be focused for all colors simultaneously. The red shouldn’t be in focus but the blue out of focus. So you have to come up with a pattern that scatters all the colors in the same way so they go into the same spot. And our technique is able to come up with a crazy pattern that does that.
Steven Johnson, Professor, Applied Mathematics and Physics, Department of Mathematics, MIT
As the next step, the scientists are working with engineers who can develop the complex patterns that would be mapped out by the new computational technique to create large metasurfaces, possibly for more accurate cellphone lenses and various other optical applications.
These surfaces could be produced as sensors for cars that drive themselves, or augmented reality, where you need good optics. This technique allows you to tackle much more challenging optical designs.
Raphaël Pestourie, Study Co-Author, Department of Mathematics, MIT
The study was partly funded by the U. S. Army Research Office through the Institute for Soldier Nanotechnologies at MIT.