Mar 10 2017
Physicists from MIPT have predicted the existence of transparent composite media with unusual optical properties. Using graphics card based simulations, scientists studied regular volume structures composed of two dielectrics with close parameters, and found that the optical properties of these structures differ from both those of natural crystals and artificial periodic composites, which are currently attracting a lot of interest.
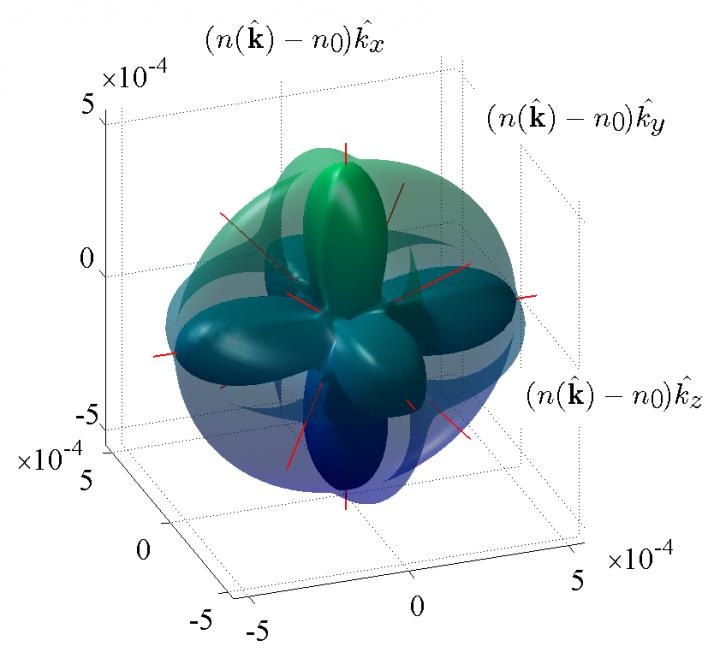This is the isofrequency surface of a cubic crystal, which always possesses seven optical axes. Axis scales are chosen in such a way to illustrate differences between the two parts of the isofrequency surface. In fact, for most crystals, both parts of the surface are almost spherical and practically indistinguishable from each other. (Credit: MIPT Press Office)
The theoretical study conducted by senior researcher Alexey Shcherbakov and sixth-year student Andrey Ushkov, who both work in the Laboratory of Nanooptics and Plasmonics, is devoted to specific composite media that were simulated by means of an approach elaborated by the group. These media allow for the existence of an effect called birefringence -- when illuminated by a light beam, the original beam splits in two inside the medium. In their article published in Optics Express, the physicists predicted the existence of composite crystal structures of a new type, in which birefringence occurs in a rather different manner to the way it does in natural crystals.
The splitting of a beam in two in birefringent materials is on the one hand due to the dependence of the properties of a crystal on the direction of light wave propagation, and on the other hand due to the presence of polarization of light waves. Polarization is the direction of the electromagnetic field oscillations in the wave, and ordinary light (e.g. from the sun or a lamp, but not from a laser) is a chaotic mixture of waves with different polarizations.
To understand what polarization is, imagine a long rope attached at one end to a wall. If someone stretches the rope and starts to periodically move the free end of the rope, waves will appear. The free end can be moved either horizontally or vertically. The whole rope would then move either in a horizontal or vertical plane respectively, and these are the two different polarizations of waves in the rope.
When the light propagates through a birefringent crystal, some of the waves with one polarization shift in one direction, whereas the others, with another polarization, shift in a different direction. Using this property, one can use the crystal to filter partly or fully polarized light depending on the polarization state of the initial incident beam. This phenomenon could have been used by Vikings, who detected the position of the sun in a cloudy sky with Iceland spar. Nowadays, birefringent crystals are widely used in laser techniques.
The theory of birefringence operates with two important concepts: optical axis and isofrequency surface. The first term refers to a direction in the crystal in which the incident wave does not split in two. For example, Iceland spar has a single optical axis, and salt crystals have none as they do not possess birefringence. There are materials with two optical axes, such as Glauber's salt, the basic constituent of which (sodium sulfate) is widely used in the glass industry and detergent manufacture. Within classical crystal optics, excluding magnetic and gyrotropic (related to polarization rotation) effects, all crystals are divided into three types: isotropic, and anisotropic with one or two optical axes.
The second concept, namely isofrequency surface, illustrates the dependence of the speed of light in a crystal on spatial direction. This surface is drawn in such a way that the length of a vector starting from the coordinate frame origin and ending at a surface point equals the ratio of the speed of light in a vacuum to the speed of light in the crystal in the direction indicated by the vector. The isofrequency surface of an isotropic crystal is a sphere whose radius is equal to the crystal refractive index since the light propagates in an isotropic medium at the same speed in any direction. The refractive index of transparent materials is always greater than unity.
For birefringent media, the shape of the isofrequency surface differs from the sphere. Moreover, the surface itself looks as if it consists of two parts, an inner and an outer part. These two parts illustrate how slower the light propagates in the crystal than in a vacuum in each direction for two different light polarizations. Points where the parts of the surface intersect indicate the optical axes, directions in which the speed of light does not depend on the polarization. The figure below shows isofrequency surfaces for salt, Iceland spar and Glauber's salt.
Beyond classical crystal optics, the basics of which are commonly taught to physics students, it appears that even crystals with a simple cubic lattice, such as salt, are optically anisotropic, i.e., the light there propagates in different directions differently. In the simplest case, this anisotropy was described by Hendrik Lorentz in the early 20th century. As many as seven optical axes were found in such crystals. This effect was confirmed experimentally in the late 20th century when scientists began to widely use lasers in research. However, the two parts of the isofrequency surface appeared to be almost indistinguishable (a relative difference of an order of 10-5-10-6), so that such anisotropy practically vanishes. In modern technologies it is only taken into account in ultra-high-precision optical projection mountings for deep ultraviolet nanolithography, which is used in modern microelectronic fabrication.
In addition to natural crystals, such as birefringent Iceland spar, scientists are able to manipulate the crystal structure using artificial materials. Advances in micro and nanofabrication during the last two decades pushed studies of these artificial materials, including metamaterials and photonic crystals, toward the edge of optical science. The regular atomic or molecular arrangement is replaced by a regular geometric pattern in these structures. This pattern can be compared with an ornamental design on a wooden jewel box, but in three dimensions and with a scale from dozens of nanometers to hundreds of micrometers.
Artificial regular structures, photonic crystals and metamaterials can exhibit rather unusual optical properties, which dramatically differ from the properties of natural crystals. For example, periodical structuring at micro and nano scales enables scientists to overcome the diffraction limit on microscope resolution, and create flat lenses. Metamaterials can have a negative refractive index and be strongly optically anisotropic. The new article by Alexey Shcherbakov and Andrey Ushkov bridges the gap between natural crystals and the mentioned artificial photonic materials, and describes optical composites which on the one hand cannot be described within the scope of classical crystallography, and on the other hand are not traditional photonic crystals or metamaterials.
The authors of the newly published research used their own model and method, which they ran on NVidia graphics processing units, to simulate composite dielectrics periodically structured in three dimensions, i.e., a 3D lattice of two transparent materials. In contrast to metamaterials and photonic crystals, where the optical contrast between lattice constituents is strong, MIPT physicists studied a combination of low refractive index and low optical contrast media with a relatively small period, about one tenth of the wavelength. Despite the fact that this combination was not commonly implicitly assumed to yield any interesting effects, the research demonstrated that some interesting physical phenomena were overlooked.
For low values of periods of investigated structures their optical properties are indeed indistinguishable from the optical behavior of natural crystals: composites with a cubic lattice are practically isotropic, whereas composites with, for example, tetragonal and orthorhombic lattices display uniaxial and biaxial properties. However, increasing the period while keeping valid the description of the composite as an effective medium, as the authors demonstrated, can cause very unusual behavior.
First, there appear new optical axes (up to ten axes in an orthorhombic crystal). Moreover, while the directions of optical axes are fixed within classical crystallography, the directions of some of the new optical axes turn out to be dependent on the period to wavelength ratio. Second, in the direction where the maximum difference of the speed of the light for two polarizations occurs for small periods (the maximum distance between the two parts of the isofrequency surface), this difference can practically go to zero, or, in other words, the direction can become an optical axis, at a certain relatively large period. Besides, owing to the use of the rigorous method, the authors obtained quantitative assessments on the validity of the effective medium approximation.
"Scientists actually mentioned that it may be possible for a crystal to possess numerous optical axes in the mid-20th century - this was stated, for example, by the Russian Nobel prize winner Vitaly Ginzburg. However, in natural crystals such effects are impossible due to the smallness of the period, and there were no technologies to fabricate a good quality composite. Additionally, the power of computing machines was also insufficient to estimate the necessary corrections to anisotropic dielectric permittivity coming from lattice anisotropy. Our result is based on the joint use of modern methods of computational physics together with the high computing power provided by graphics cards. In our work we also developed an approach which allows us to calculate an effective optical response of a complex composite with controlled precision by virtue of so called first principle calculations (in our case a rigorous solution of Maxwell's equations)," said Alexey Shcherbakov describing the results.
Possibilities for practical applications may come after experimental validation of the theoretical predictions. Modern technologies allow in principle the fabrication of composites of interest for operation in various optical bands. For example, 3D high resolution multiphoton lithography can be used for the infrared band, whereas for the terahertz band one can apply microstereolithography. The discovered effects make artificial crystal anisotropy strongly dependent on the radiation wavelength, which in not the case for transparent natural crystals. This may enable scientists to develop new types of optical polarization control elements.