Atomic force microscopy (AFM) is a powerful tool for studying biologically relevant soft materials.

Image Credit: Elizaveta Galitckaia/Shutterstock.com
Understanding the viscoelastic properties of soft biological samples is essential. Studying the underlying dynamics of such samples is driven by their correlation with disease and cellular transformation. Viscoelastic materials exhibit mechanical properties that are both like elastic solid and viscous liquid.
Methods for Studying Viscoelasticity
Many experimental techniques have been developed for measuring cellular mechanical properties, including optical tweezers, micropipette aspiration, cell traction force microscopy, and magnetic twisting cytometry. However, atomic force microscopy (AFM) has emerged as the most popular method for imaging the mechanical properties of soft samples such as cells and tissues. AFM allows for a broad range of techniques that can be applied for characterizing biological samples.
Underlying Principles of AFM
In AFM, a cantilever with a tip is used as a force sensor. The tip is moved vertically into the surface of a soft sample to measure interactions between the sample surface and the tip.
As seen in figure 1 (a), the back of the cantilever is coated with a reflective substance. The reflection of a laser beam shone onto the back of the cantilever is detected by a photodetector. The cantilever can be moved electrically so that the tip can either drag across the surface or indent the sample. AFM indentation experiments provide a suitable platform to measure viscoelasticity.
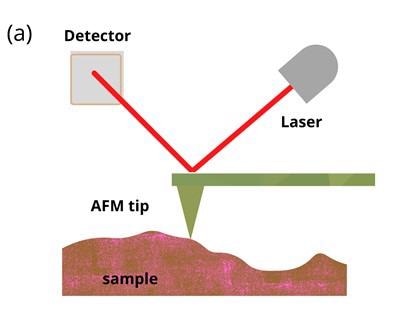
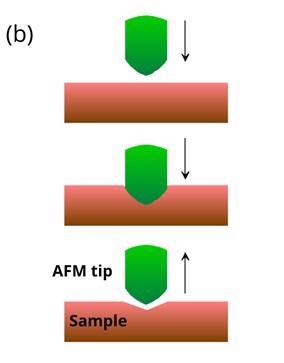
Figure 1: Schematic illustrations of (a) basic principles of AFM and (b) AFM indentation method where the tip is moved vertically into the sample before being retracted. Soft samples show hysteresis when probed. Image Credit: Ilamaran Sivarajah
In an AFM indentation experiment, the tip is moved towards the sample with a predefined vertical speed as illustrated in figure 1 (b). After the tip makes contact with the surface, the tip starts to indent the sample until a pre-set length or force is achieved. The cantilever is then retracted at the same speed. Based on the deflection detected during the approach and the retreat of the tip, valuable information about the sample can be calculated.
Analyzing AFM Data
Data from AFM indentation experiments produce force versus displacement curves. A conventional mathematical model used to analyze the approach and retraction force curves is the Hertz model.
With the Hertz model, Young's modulus of the sample under investigation can be calculated. The Young's modulus is a property of any material that can easily stretch or deform. It is defined as the ratio between stress and strain of the material.
Young’s modulus can be calculated by measuring the distance a material stretches when a force is applied. An AFM indentation experiment provides the force and displacement information necessary to fit the Hertz model.
Limitations of the Hertz Model
The Hertz model approximates the sample as an isotropic and linear elastic solid. The Hertz analysis also does not consider any hysteresis of the sample when probed. However, living cells and most other biological materials undergo hysteresis and are also heterogeneous and anisotropic.
Anisotropy describes the physical property of exhibiting different values when measured along different directions. To predict, measure, and analyze viscoelastic samples better, different AFM experimental techniques and more comprehensive theoretical models have been developed.
Operational Modes of AFM
AFM offers a variety of operational modes that are conducive for measuring viscoelasticity. Methods for measuring viscoelastic properties with AFM can be divided into two modes. In the first method, called static mode, the tip moves vertically while indenting the sample as described previously.
In static mode, the tip can also be dragged across the sample surface. The second method is called the dynamic mode. In the dynamic mode, the tip on the AFM cantilever is oscillated at a controlled frequency. This leads to oscillatory deformations of the sample. Images with high resolution can be obtained using the dynamic operational mode.
New Models for AFM Analysis
A range of mathematical models have been developed to analyze the data acquired by the different AFM experimental techniques. Due to the complex nature of active cells and other biological soft materials, rigorous computational methods are required.
The choice of model depends on the structure of the sample studied. These methods rely on the force-displacement curves but also take into account the variables associated with the physical properties of soft samples, for example, models based on the elastic-viscoelastic correspondence principle, Standard linear solid (SLS) model and Kelvin–Voight and Maxwell models.
Challenges and Limitations
Viscoelastic measurements acquired using AFMs can be affected by numerous uncertainties. Depending on the operational methods employed and the structures studied, there can be large variations in the results.
Factors such as AFM tip geometry, deflection sensitivity, and electromechanical devices used for control can affect the experimental outcomes.
Standardized procedures for data acquisition and analysis have significantly improved the consistency and reproducibility of viscoelastic measurements.
AFM combined with other techniques has become a valuable tool for the imaging and studying of viscoelastic materials. With the various predictive and analytical models being developed, AFM is a powerful tool for diagnosis, treatment, and regenerative medicine.
References and Further Reading
Efremov, Y.M., Wang, WH., Hardy, S.D. et al. Measuring nanoscale viscoelastic parameters of cells directly from AFM force-displacement curves. Sci Rep 7, 1541 (2017). https://doi.org/10.1038/s41598-017-01784-3
Chim, Y.H., Mason, L.M., Rath, N. et al. A one-step procedure to probe the viscoelastic properties of cells by Atomic Force Microscopy. Sci Rep 8, 14462 (2018). https://doi.org/10.1038/s41598-018-32704-8
Y. M. Efremov, T. Okajima and A. Raman, Soft Matter, 2020, 16, 64 —81. DOI https://doi.org/10.1039/C9SM01020C
Lu Y.-B., Franze K., Seifert G., Steinhäuser C., Kirchhoff F., Wolburg H., Guck J., Janmey P., Wei E.-Q., Käs J., Reichenbach A.: Viscoelastic properties of individual glial cells and neurons in the CNS, PNAS 103:17759-17764, November 2006
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.