A wide range of measurement systems is available for the optical characterization of MEMS devices. This follows an array of technologies that are available for measuring many different physical properties (such as film thickness, dimension, cross section, step height, stress, roughness modulus elasticity, stiction, response time, resonance frequency, thermal expansion, and so on). For instance, dimensional analysis and deformation measurement can be performed through basic optical microscopy equipped with digital image processing.
More sophisticated optical measurement systems are customized toward particular capabilities (for example, dynamic response, 3D shape measurement, high lateral resolution, and/or high vertical resolution). A comparison of commonly available methods is shown in Table 1.
Table 1. Comparison of MEMS optical measurement tools
| Technique |
Lateral Resolution (typical) |
Vertical Resolution (typical) |
Static Shape |
Dynamic Response |
Realtime Response |
| AFM (Atomic Force Microscopy) |
0.0001 µm |
0.0001 µm |
3D |
No |
No |
| SEM (Scanning Electron Microscope) |
0.001 µm |
- |
2D |
No* |
No |
| OM (Optical Microscopy) |
<1 µm |
<1 µm |
2D |
No* |
No |
| CM (Confocal Microscopy) |
<1 µm |
<0.01 µm |
3D |
No |
No |
| WLI (White-light Interferometer) |
<1 µm
<0.01 µm ** |
<0.001 µm |
3D |
Yes** |
No |
| DHM (Digital Holographic Microscopy) |
<1 µm
<0.01 µm ** |
<0.001 µm |
3D |
Yes** |
No |
| SVM (Strobe Video Microscopy) |
<1 µm
<0.01 µm ** |
<1 µm |
2D |
Yes** |
No |
| LDV (Laser Doppler Vibrometry) |
<1 µm
<10-6 µm *** |
<10-6 µm *** |
No |
Yes |
Yes |
*Dynamic response possible using video capture technique
**Dynamic response possible using strobe technique
***Resolution for real-time dynamic response — not static
The real-time capability of a laser Doppler vibrometer (LDV) enables measurement times about six orders of magnitude smaller in comparison with any method based on strobe techniques, or provides a similar measurement time and an amplitude resolution of about 6 orders of magnitude or even better.
Polytec Optical Measurement System
The optical measurement system available from Polytec has been specifically designed for measuring dynamic response. Most often, in MEMS devices, elements meant for actuation and sensing purposes have to be actively moved. Crucial information offered by dynamic response measurements cannot be established through electrical testing alone. Some examples of dynamic response measurements are resonance frequency of cantilevers, displacement amplitudes of resonators, and settling time dynamics of micro-mirrors. Here, non-invasive measurement methods that are precise, high-resolution, and real-time are required.
Within the Polytec microscope-based measurement system, three technologies are used, such as LDV, strobe video microscopy, and white-light interferometry (WLI). LDV is used for measuring out-of-plane motion. In-plane motion measurements are made by adding two extra vibrometer channels angled to the surface. Deflection shapes can be determined and shown as 3D animations through automated scanning. Strobe video microscopy — another method for measuring in-plane motions — again extends the analysis to the planar direction to offer a complete 3D motion measurement. WLI adds the potential of surface topography measurement for static shape.
The MEMS community is currently using this instrumentation to characterize a range of devices like cantilevers, micro-mirrors, actuators, accelerometers, gyros, ultrasonic transducers, RF switches, microphones, inkjets, resonators, and pressure sensors. Applications include:
- Characterization of device response at the time of design development and release processes
- Dynamic testing of device response to establish mechanical parameters like stiffness, damping, and resonant frequency
- Design validation of performance against expected predictions of the FE model
- Calibration of sensor and actuator displacements against drive voltage across an array of frequencies and motion
- Measurement of settling time dynamics to establish the exact movement against time and display 3D visualization of response
- Topography measurement to establish surface properties after a fabrication process, such as geometry, shape, roughness, curvature, film stress, step height, and delamination
This article explains the application of the Polytec optical measurement system in some of the aforementioned examples. The principles of operation are significant for inferring the innate advantages and drawbacks of the technology used. An in-depth synopsis of this technology is given in this article, with a number of examples to demonstrate how the aforementioned methods are applied for important applications.
Laser Doppler Vibrometry
The LDV is an optical instrument that uses laser technology to determine displacement and velocity at chosen points on a vibrating structure. Laser vibrometers enable non-contact measurements and are not affected by environmental conditions or surface properties. The laser beam can be directed to a spot down to 1 µm in diameter, enabling the analysis of MEMS structures that are visible under an optical microscope. Diffraction limitations tend to impact the measurements of devices that are smaller than the wavelength of the used light (532 nm).
LDV is a highly sensitive optical method that has an overall ability to measure displacements from centimeters to picometers at frequencies from near DC to gigahertz. The LDVs, besides their broad frequency range, also possess a wide dynamic range (more than 170 dB) for velocity amplitudes ranging between 0.02 µm/second and 10 m/second. These aspects enable measurements that otherwise cannot be done using holographic or other methods.
The LDV makes use of the Doppler effect, in which light backscattered from the moving target carries information related to the motion quantities, displacement, and velocity at the point of incidence. Surface displacement modulates the phase of the light wave, while instantaneous velocity moves the optical frequency. The light wave, thus received, is combined with a reference beam with the help of interferometric methods so that both the beams recombine at the photo-detector. Figure 1 shows the basic schematic structure of a modified Mach-Zehnder interferometer.
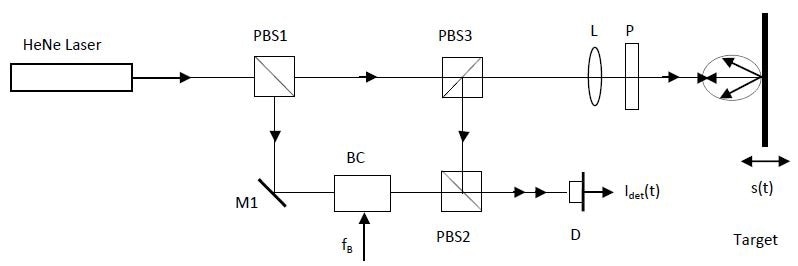
Figure 1. Optics schematic of a modified Mach-Zehnder interferometer
Phase modulation and direction sensitive frequency from the moving target are carried by the signal determined at the photo-detector. Target displacement s(t) leads to a phase modulation
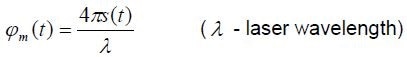 |
(1) |
In accordance with the basic relationships, dφ/dt = 2πf and ds/dt = v, that phase modulation matches with a frequency deviation referred to as the Doppler frequency.
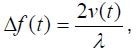 |
(2) |
The ensuing frequency of the detector output signal accurately maintains the directional information (sign) of the velocity vector.
The measurements made through the LDV technique are dynamic by nature and do not carry any information regarding the static shape (as is possible using other methods such as white-light interferometry or digital holography). Both velocity and displacement are encoded in frequency and phase modulation of the output signal of the detector. Phase and/or frequency demodulation methods are employed in the signal decoder of a laser vibrometer to recover the velocity and displacement time histories from the modulated detector signal.
Both analog and digital frequency demodulators directly change the instantaneous Doppler frequency into voltage that is in proportion to vibration velocity. Sensitivity, critical accuracy, signal-to-noise ratio, and linearity are provided by the high-quality demodulation electronics, ensuring a complete vibrometer system.
It is possible to extend the LDV measurement instruments to a 3D vibrometer setup, allowing pm-resolution for both in-plane and out-of-plane motions. The optical configuration is based on heterodyne Mach-Zehnder interferometry that contains three linearly independent interferometer paths (see Figure 2). The laser beam, which is directed on-axis via the main interferometer, is frequency-shifted acousto-optically with regards to the three reference beams by a Bragg-cell. Subsequently, the scattered light is collected on-axis and also in two off-axis directions. The entire broad-bandwidth 3D vibration spectra at the measurement spot are contained in the three detector signals, and the vibration data in Cartesian coordinates is derived using a coordinate transformation.
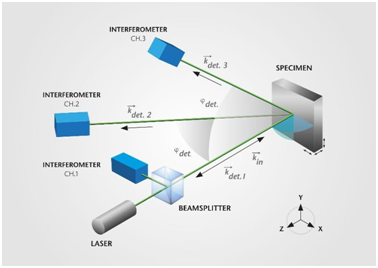
Figure 2. Optical layout of 3D laser vibrometer
However, LDV has one major disadvantage — the measurements are made at a single point and not captured on a full field as is the case using video interferometry methods. The LDV technique can be extended to full area scanning by using scanning mirrors to deflect the laser measurement beam in both x and y directions. The schematic for this is illustrated in Figure 3 with scanning mirror M. It is possible to position the laser measurement beam to any point visible on the live microscope video. This method is used for scanning an area point by point to determine the structure’s velocity field. Although a single-point LDV can be treated as a standard sensor (that is, analog output recorded by data acquisition systems, including an oscilloscope), the scanning LDV needs system software to produce a scan measurement grid, to control the scanning process, and to concurrently acquire the measurement data.
The phase of each point is established by concurrent measurement of an additional reference channel (generally, the drive signal created by the internal signal generator). Based on this data, the 3D deflection shapes are quantified. The final result includes mapping of the velocity mapping and/or mapping of the displacement field over the structure that enables 3D animations of the response either in the time or frequency domain (see Figure 2 and Figure 4).
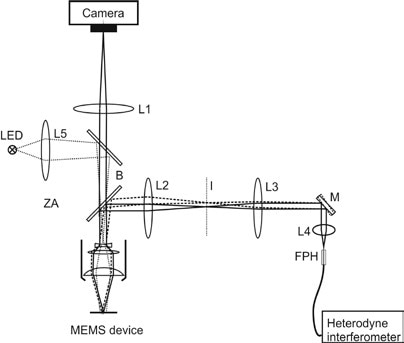
Figure 3. Optical layout of microscope scanning laser vibrometer
Strobe Video Microscopy
MEMS’s in-plane periodic motion is measured using strobe video microscopy. This method can be used in tandem with LDV. The stroboscopic images are captured by an integrated CCD camera, as illustrated in Figure 4. The LED-strobe flashes, the signal driving the specimen, and the camera exposure have to be accurately synchronized. Figure 4 shows a timing diagram of the strobe synchronization for two camera shots at two varied phases in relation to the periodic excitation.
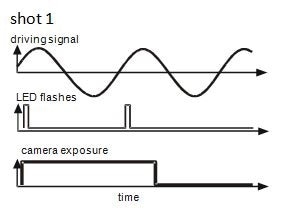
Figure 4. Timing diagram of the strobe signals
After obtaining a data set containing strobe images, pixel deviations between frames are established by machine vision analysis. In-plane motion algorithms compute the position shifts (δx, δy) of a user-defined search pattern between successive images via correlation functions. It is possible to calculate the values of δx and δy down to sub-pixel resolution by using image-correlation methods. However, this needs post-processing and is not captured in real time, as done for the LDV.
The pattern match as well as the displacement of a comb drive MEMS device at resonance is depicted in Figure 5. The system automatically steps through user-defined frequencies, and this is followed by recording the image sets to obtain frequency response. For each measured frequency, displacement vs. phase delay data is extracted and shown as a Bode plot. In-plane motion analysis can be conducted with sine excitation and also for a step response.
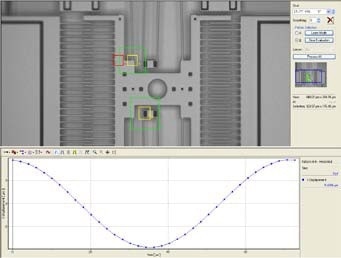
Figure 5. In-plane motion of comb drive device
White-Light Interferometry
White-light interferometry, or WLI, in short, enables static surface topography measurements. This offers an x-y-z mapping of the surface of the device to establish vital parameters like curvature, flatness, roughness, step heights, angles, volumes, and parallelism. The outcome can be shown as 2D or 3D mappings for defect analysis, evaluation, and/or processing to extract parameter values for specified areas.
By applying the optical configuration depicted in Figure 6, the WLI is performed using a Michelson interferometer. The white-light source employed has a coherence length in the micrometer range. Furthermore, the collimated light beam is split at a beam splitter into a reference beam and an object beam. The light, which is scattered back from the object and the mirror respectively, is superimposed at the beam splitter once more and imaged to the CCD camera. This interference leads to the formation of a fringe pattern that is mapped out for every pixel in the camera image.
When the position interference lens is moved using a Z-stage, the interference signal is modulated for every pixel, leading to a correlogram. The highest value of the correlogram emerges when the distance to the reference mirror is exactly equivalent to the distance to the surface of the device. After a measurement run, the correlograms from the camera frames are examined, and the surface’s true topographical representation can be reconstructed as a 3D topography map, as depicted in Figure 7.
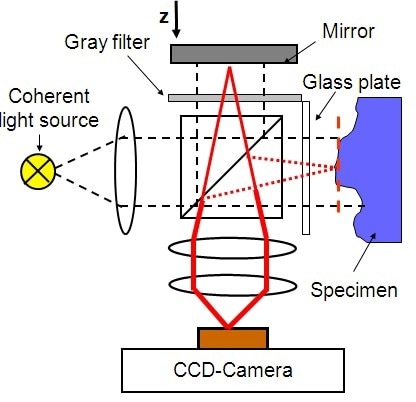
Figure 6. White-light interferometer schematic

Figure 7. Topography measurement of a micro gearwheel
Application — Texas Instruments Digital Mirror Device (DMD)
Settling time is a vital parameter for the micro-mirror applications in which the orientation of the mirror is quickly changed from one tilt state to another. Here, accuracy and speed are the main performance indicators. The mirror design has complex factors like resonance frequencies, damping coefficients, and optimization of drive control signals that affect the settling time response. LDV can be used for measuring these factors for real-time response with high accuracy and sampling rate. 3D visualization of mirror response is provided by scan measurements as time animated sequences.
Measurements are made on Texas Instruments DMD arrays. The array contains countless numbers of 12 μm mirrors. As shown in Figure 8, each mirror rotates by ±12° about a primary axis by twisting about a concealed hinge. By shifting the mirror from “−” to “+” state, the illumination projected for an individual pixel can be regulated, and the gray level brightness can be regulated by the amount of time at the “+” state.
The mirrors have the potential to switch on/off at a speed of about 50,000 times per second. The range of color scales available in the projected image can be increased by further enhancing the switching speed.
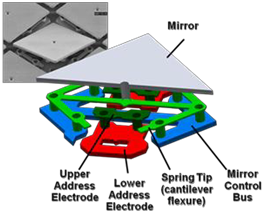
Figure 8. Structure of a Texas Instruments micro-mirror
Using the LDV technique, scan measurements are taken on the DMD array to determine the settling time response and offer a 3D time visualization of movement. Shown in Figure 9 is the displacement of a point targeted by the laser measurement spot at the corner of the mirror.
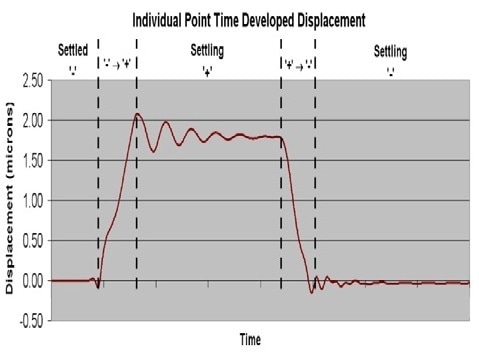
Figure 9. Time response of an individual point on a mirror
When the corner of the mirror is transitioned to the “+” state by rotating 12°, it is displaced upward and needs a characteristic time to settle to a stable orientation. At the time of the settling, the mirror has a damped oscillation at the basic torsional resonance. When this measurement is repeated at coordinate locations over the entire surface, a complete 3D dynamic representation of the movement of the mirror is established for the primary tilt motion, along with the orthogonal roll and sag motions.
The outcome is a 3D animation demonstrating the accurate time sequence for all the three axes. Extending the measurement over multiple mirrors in the array makes it possible to compare the relative phase of the motion from one mirror to another. These measurements served as an important gage of design settling time performance and are used for guiding the design development of the future.
Application — Testing Pressure Sensors on Wafer Level
Wafer-level testing can offer an effective method of quality control and bring down the costs associated with packaging MEMS devices that do not satisfy the specifications. Identification of material and geometrical parameters using LDV offers real-time measurements that can be rapidly automated at the wafer level on a probe station. The measurement microscope head used can be easily mounted on any kind of probe station. It is possible to determine the resonance frequency at a single point on the structure in just milliseconds.
The probe station shifts to the next device and the same measurement is again made. The process takes about 2 seconds per die, and the final result is a wafer map showing quantitative estimated identification error used for “pass/fail” criteria.
Measurements are made for pressure sensors containing 1300 µm x 1300 µm devices, processed through KOH etching. A membrane thickness algorithm — based on frequency response measurements carried out by LDV — is employed as the basis for parametric testing. Contactless electrostatic probes are used to excite the membranes. Shown in Figure 10 is the frequency response of two devices — the first one displays the frequency response of a “good” die with resonances at predicted frequencies (Figure 10A), and the second one reveals the frequency response of a “bad” die with shifted resonance frequencies (Figure 10B).
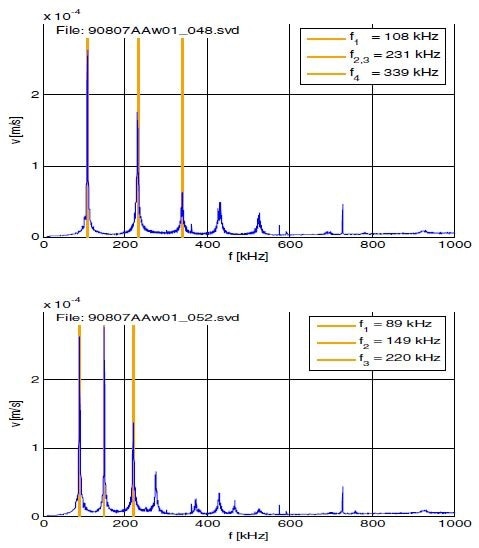
Figure 10. (A, upper): Frequency response of good device. (B, lower): Frequency response of bad device.
Calculation of an estimated identification error (EIE) offers a quantitative evaluation that makes it possible to classify processing errors. As depicted in Figure 11, these are mapped on the wafer, with criteria for maximum error applied to screen out the “bad die” (indicated in red).
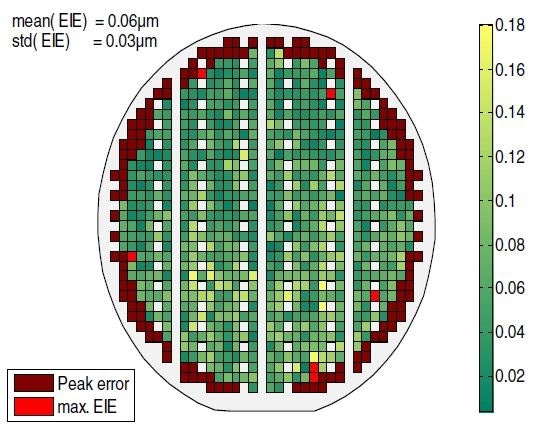
Figure 11. Wafer map of Estimated Identification Error. Bad Devices are shown in red.
Application — FE Model Validation
FE models are applied to simulate mechanical response during the design phase of MEMS devices. Standard models take in intricate mechanical and electrical parameters to predict device response and are used for designing the device toward target specifications. Since the majority of these parameters have variations owing to fabrication processes, testing should be done to validate them. This is particularly true at the initial fabrication phases, wherein the process is not suitably controlled and more uncertainties exist. Shown below is a basic example of a MEMS cantilever beam. The silicon beam measures 40 μm wide, 225 μm long, and 4 μm thick. The resonance frequency f is given by:
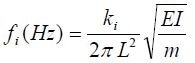 |
(3) |
where L refers to the length, E refers to the elasticity, m is the mass, and I is the moment of inertia. An ANSYS model of the silicon beam is obtained using 1000 node points on the basis of the modeled geometry. The first bending mode is predicted to appear at 94,153 Hz (see Figure 12, right). This model is experimentally confirmed using scanning LDV measurements on the beam, through the same density of measurement points as node points for the model. Next, the experimental results are compared for validation, followed by updating the model based on the data.
Complex effects like non-uniformities, geometric errors, residual stress, damping, torsional compliance, and mismatching boundary conditions are usually not considered in an idealized model. Here, the experimental results offer the first bending mode at a lower frequency of 66,718 Hz (see Figure 12, left). Conversely, this is explained by inaccurate geometrical values used in the model.
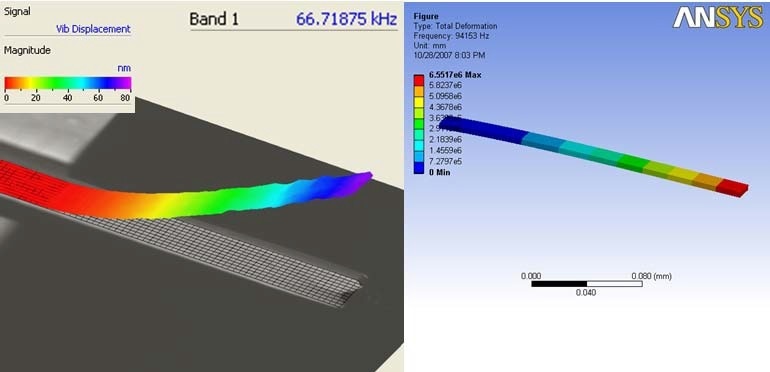
Figure 12. Comparison of cantilever first bending mode determined experimentally (left) and from FE model (right).
With regards to inertial sensors, modeling can be more complicated for sense and drive modes using, for instance, tuning fork or comb drive resonators. These modes are often designed at particular frequencies that have to be validated through experimental measurements.
Application — Optimizing the Design of Accelerometers
MEMS devices have built-in mechanical and electrical components to form electro-mechanical systems. During the characterization and troubleshooting of these devices, it is usually hard to establish whether an observed behavior is purely electrical, purely mechanical, or innately both. LDV measurements enable direct mechanical measurements that are not affected by electrical effects.
A typical measurement is illustrated for a robust and stable MEMS low-g servo accelerometer formerly developed by Applied MEMS. The accelerometer’s noise floor is close to 30 ng/√Hz and its dynamic range is >115 dB. The sensor is designed for adverse environments of oil exploration for seismic exploration and monitoring; however, it can also be used for inertial navigation, and for vibration monitoring and analysis.
During the initial stages of development, a false resonance close to 20 kHz is observed in the accelerometer output. While this frequency is well beyond the preferred performance band, this mode is assumed to be responsible for the reduced performance of the sensor. Although the source of the mode is not known at the time, there are a number of suspected causes. Mechanical sensor modes close to this frequency are known to exist from FEA simulation, although it is not clear how these modes could manifest in the sensor’s closed-loop output. Package-induced modes and artifacts from the control loop are also regarded as a source of the 20 kHz tone.
In order to further analyze the cause of the tone, scanning vibrometry is used for scanning the bare die surface, as depicted in Figure 13. Considering that the device is a variable capacitor with forcing and sensing electrodes on both sides of the moving proof mass, it was essential to remove one of the electrode caps to scan the moving parts inside. After the de-capped die is fixed to a high-frequency shaker, it is mechanically stimulated in the band of interest.
The whole surface is scanned using broadband input to the shaker to stimulate all modes in the band of interest. This demonstrated the frequency and general location of the modes for the device being tested. This data can be used for performing higher resolution fast scans at single frequencies, for particular modes at different locations on the die.

Figure 13. MEMS accelerometer die from Applied MEMS
Figure 14 shows the results of a fast scan over a 1.5 x 1.5 mm section containing the accelerometer spring elbow. The peak displacement of the spring elbow measures 800 nm. Through this scan, a mechanical resonance of the spring elbow can be vividly observed. Since only mechanical excitation was used to perform the LDV measurement, it is feasible to further eliminate the electrical causes of the spurious mode. In addition, the scan shows additional higher order modes of the spring arm at frequencies nearing 1 MHz. Therefore, the negative effects of this mode are brought down by redesigning the sensor. The resultant sensor designs not only improve device performance but also result in higher yields.

Figure 14. Bending mode of flexure at 23 KHz
Conclusion
The valuable optical measurement tools provided by Polytec can be used for the research and development of MEMS devices applied in real-world applications. Through Laser Doppler vibrometry, broadband and real-time measurements of dynamic response with a resolution down to the picometer level can be realized. The aforementioned examples explained in this article demonstrate its application for the design optimization, characterization, and troubleshooting of the Texas Instruments DMD array and applied MEMS accelerometer.
Additionally, it is possible to extend the capability to fast, automated production test measurement on the wafer level. The application of measurement methods exclusively gives an inside view of MEMS devices, enhances performance and yield, shortens design cycles, and eventually reduces the product cost.

This information has been sourced, reviewed and adapted from materials provided by Polytec.
For more information on this source, please visit Polytec.