A team led by Professor Yiqi Zhang of Xi’an Jiaotong University and Professor Yaroslav V. Kartashov of the Russian Academy of Sciences collaborated to experimentally write two distinct kinds of Sierpinski gasket fractal waveguide arrays in fused silica samples using femtosecond laser direct writing technology for the first time in a recent study published in Light: Science & Applications.
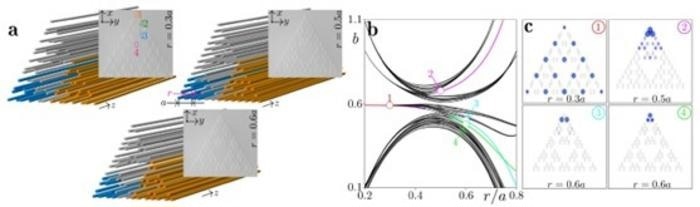
(a) Schematic representation of the third generation of the Sierpinski gasket waveguide arrays with r=0.3a, 0.5a, 0.6a. Blue and orange sectors of these arrays represent the first and second-generation structures respectively. Microphotographs of the corresponding fs-laser written waveguide arrays are presented in the insets. (b) Eigenvalues of the stationary linear states vs distortion parameter. (c) Intensity distributions for four representative eigenstates. Image Credit: Hua Z. et al.
Fractals are aperiodic, self-similar structures found throughout the universe. They are characterized by their lack of bulk and non-integer effective Hausdorff dimension. Although they have not been observed experimentally in topological photonic systems, fractal HOTIs have been proposed in electronic and acoustic systems.
Nonlinearity in photonic systems can lead to geometrical frustration and mobility control around the Fermi level. It can also effectively tune the propagation constants of nonlinear modes within the spectrum of the topological photonic system, resulting in complex and qualitative changes in its internal structure.
Consequently, topological systems can be constructed with greater adjustability by adjusting the nonlinear power. By incorporating this unique fractal structure into nonlinear photonic systems, new avenues for light control and localization research could become possible.
The team investigated the interaction between topological modes and nonlinear effects to obtain topological corner solitons and experimentally and numerically realized the aperiodic photonic fractal HOTI. In addition to producing much richer soliton families and dynamics, the reported method and technique also create new opportunities for future light control on aperiodic systems.
The research team constructed aperiodic fractal HOTIs on two varieties of Sierpinski gasket waveguide arrays. The structures are displayed in the above image. Fractal arrays have several holes, inner corners, and edges because of their construction, and their effective Hausdorff dimension is a fraction.
The research team also fixed the distance between the fractal arrays and introduced a shift parameter r to modify the coupling strength between adjacent waveguides. This can significantly alter the energy spectrum and yield the topological corner states. In contrast to periodic HOTIs, the topological states in Figure 1b are found in the r>0.5a and r<0.5a domains (see the colored curves). The linear spectrum is plotted against the distortion parameter.
The others represent coexisting outer corner states with distinct internal structures, while the red branch represents hybrid corner states. The research team also determined the real-space polarization index to characterize the system's topological properties as fractal waveguide arrays are aperiodic structures and lack bulk.
The corresponding findings show that fractal structure can support topological nontrivial modes in entire space. Figure 1c displays the intensity distributions of the four common localized states corresponding to the circles in Figure 1b. This rule covers the next and higher-order structures.
The research team used the Newton method to study the focusing nonlinear topological corner spatial soliton families in nonlinearity and localized corner states in fractal arrays. They demonstrated a strong correlation between the nonlinear propagation constants and the localization of thresholdless corner solitons. Rapid power increases cause the solitons to broaden gradually and the localization to weaken. The solitons may spread to the entire array when the propagation constants approach the edge of the extended states.
The research team chose four representative locations to investigate the excitation dynamics of the nonlinear corner states under variable energy pulses. They looked into whether well-localized thresholdless hybrid corner states could be supported in any inner or outer corner by the structure of r=0.3a.
Although the gap width is relatively small in the array with r=0.5a, even slight changes in pulse energy can result in significant changes in the output intensity distribution, which may require higher pulse energies to reach a similar level of localization.
Only thresholdless outer corner solitons contained in three closely spaced outer corner waveguides can be formed by the three linear outer corner modes supported by the array with r=0.6a. In contrast, there is good agreement between the experimental and theoretical results.
The research team presented the first example of nonlinear aperiodic photonic fractal HOTI that can support a wide range of topological corner states. The remarkable new feature of the fractal structures considered here is that they have corner states for a broad range of distortion parameters, far exceeding the range where higher-order topological phases appear in periodic HOTIs.
These findings can be applied to new designs of topological or on-chip lasers, extending the class of HOTIs while highlighting new avenues for exploring and utilizing nonlinear phenomena in photonic fractals.
Journal Reference:
Zhong, H. et. al. (2024) Observation of nonlinear fractal higher order topological insulator. Light: Science & Applications. doi.org/10.1038/s41377-024-01611-1