In confocal Raman imaging the acquisition time for one Raman spectrum is a crucial value, as it influences the acquisition time of the image which typically consists of tens of thousands of Raman spectra. This article describes how the use of a spectroscopic EMCCD as the detector can significantly reduce the acquisition time down to a few milliseconds per spectrum, as well as tremendously improving sensitivity.
Working Principle behind Confocal Microscopy
Confocal microscopy uses a point light source (laser) which is focused onto the sample. The reflected (fluorescence) light is usually collected with the same objective and focused into a pinhole in front of the detector. This ensures that only light from the image focal plane can reach the detector, which strongly increases image contrast and, with proper selection of pinhole size, slightly increases resolution.
In confocal Raman imaging, as in the alpha300 R system which was used for the experiments described here, special filters are used to suppress the reflected laser light while enabling the Raman scattered light to be detected with a spectrometer/ CCD camera combination. To obtain an image, thousands of spectra are acquired in a very short time with typically less than 100 ms integration time per spectrum.
As the Raman scattering cross section is very small and the excitation power is limited to a few milliwatts, how can one improve the overall sensitivity of a confocal Raman system?
Optimizing S/N Ratio Improves Overall Sensitivity of CRM System
The important factor to optimize is the signal-to-noise ratio (S/N). The first step is to improve the collected Raman signal. This can be done by optimizing the throughput of the microscope and spectrometer and by using an objective with a high numerical aperture (NA). The confocal setup helps to reduce unwanted background signal from out-of-focus areas and further enhances S/N.
The Use of an Appropriate Detector with the Highest Sensitivity
Next is the choice of an appropriate detector with the highest sensitivity, such as a back-illuminated CCD, which can have a quantum efficiency of more than 90%. The main sources of noise of the detector itself are the dark noise and the readout noise. The goal must be to eliminate all other noise sources, so that only the photon shot noise remains.
As photons follow the Poisson statistic, for a given signal the uncertainty is the square root of the signal in electrons. In the absence of other noise sources, for a signal of 100 electrons, S/N cannot be greater than 10.
Dark Noise Reduces the Cooling Efficiency of the CCD
Dark noise is due to thermally generated carriers in the CCD, which can be dramatically reduced by efficient cooling of the CCD. A good CCD has a thermal dark current of less than 0.01 electrons/pixel/second at -60°C. Therefore, cooling below -60°C is not necessary for integration times of a few seconds. For integration times of less than 100 ms, as in the confocal Raman setup, dark current is completely negligible. Readout noise is produced while converting the collected electrons into digital counts and is limited by the quality of the CCD's readout amplifier, as well as the speed (digitization rate) of the readout process. Readout noise is specified by the camera manufacturer and is given in electrons. Typical values are 5-10 electrons for a 50kHz readout rate to about 30 electrons at 2.5 MHz readout rate.
The Readout Noise Limit
If the readout noise exceeds the photon shot noise, the signal is said to be readout noise limited. In normal spectroscopic experiments one would simply increase the integration time to acquire enough signals to ensure that the signal is shot noise limited again. Unfortunately, this is not always possible in confocal Raman microscopy.
If one acquires an image consisting of 128 pixels/line and 128 lines with only 1 s integration time/spectrum, the total acquisition time would be 4,5 hours, which is reduced to less than 30 minutes for a 100 ms integration time or to less than 3 minutes for a 10 ms integration time. Unfortunately, the faster the read out of the detector is, the noisier the readout amplifier gets.
A 1024x128 pixel CCD equipped with a 50 kHz readout amplifier can be read out in about 22 ms, which is also the shortest possible integration time. If we assume a readout noise of 10 electrons, every signal below 100 electrons/pixel will be readout limited (Poisson noise < readout noise). If the readout noise is 30 electrons for a fast readout amplifier, even a signal of 900 electrons (~ 1000 photons/pixel on the detector) will be readout limited.
What is an Electron Multiplying CCD
An electron multiplying CCD (EMCCD) is a normal CCD with an additional readout register which is driven with a much higher clock voltage than a normal CCD readout register. Due to this high clock voltage, an electron multiplication through impact ionization is achieved with an adjustable total amplification of the signal of up to 1000 times. With this setup, it is always possible to amplify the signal above the readout noise so that the S/N ratio is always limited by the Poisson noise of the signal, even if a very fast readout amplifier is used. As an example, a 1600 x 200 pixel EMCCD with a 2.5 MHz readout amplifier, as used for the experiments in this article, can be read out in only 2.3 ms.
Calculations Showing the Improvements in S/N for Different Signals
The following calculations show the improvements in S/N that can be expected for different signals. It is assumed that the quantum efficiency (QE) of the CCD is 90% and that the amplification of the signal is set to a value at which one A/D count equals the number of electrons of the readout noise (1 A/D count = 30 electrons for a 2.5 MHz readout amplifier).
If 100 photons fall on a CCD pixel in a given integration time, 90 electrons will be generated and converted to 3 A/D counts. The readout noise will be 1 A/D count and the Poisson noise will be 9.5, which is approximately 0.3 A/D counts. With these numbers, the S/N ratio is about 2.6.
In an EMCCD, the signal will be multiplied by the electron gain factor which can be as high as 1,000. A smaller amplification factor would generally be used, but for the calculation it does not make a difference. 90 electrons will be amplified to 90,000 electrons resulting in 3,000 A/D counts. The Poisson noise is 9,500 electrons which translate to 317 counts, while the 1 count readout noise is completely negligible. S/N is 9.5, which is an improvement of a factor of 3.6.
If the signal is only 10 photons, this will result in a signal of only 0.3 counts for a normal CCD. Poisson noise can be neglected in this case. With 1 count readout noise, S/N is 0.3, hardly a detectable signal.
For an EMCCD, the signal is 333 counts and Poisson noise is 100 counts which gives a S/N of 3.3, an improvement of 11 times over a normal CCD.
In reality the electron multiplying process itself adds an additional, so called excess noise factor of about 1.4, so that the real improvements in S/N are reduced to 2.6 and 7.9 respectively for the above examples.
For higher signals, in which the signal intensity is no longer readout limited, the excess noise factor of the EM process reduces the S/N ratio of an EMCCD to below that of a normal CCD. In this case, the EM register can be switched off and then the "normal" readout register is used. Thus, the EMCCD behaves just as a normal back-illuminated CCD.
Confocal Raman Images of Polymer Samples
Fig. 1 shows three confocal Raman images of an extremely thin PMMA film, spin-coated onto a glass substrate. In the center of the images, a vertical scratch was made with a metal needle to remove the PMMA layer. The film thickness, as measured with an AFM across this scratch was 7.1 nm. It was observed that there was an additional contamination layer of 4.2 nm thickness. The origin and material composition of this contamination layer was not known initially but could be determined by the confocal Raman measurement.
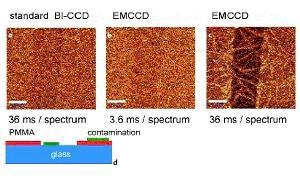
Figure 1. (a)-(c) Confocal Raman images of a 7.1 nm thin PMMA layer on glass obtained in the CH2 stretching band around 3000 / cm. Scale bar: 10 µm. (d) Schematic of the sample 30 x 50 µm, 100 x 80 pixel = 8000 spectra, 110 ms/spectrum.
The images were obtained by acquiring 200 x 200 Raman spectra in a 50 x 50 mm scan range and integrating the intensity of the CH2 stretching band of PMMA at around 3000 / cm. Excitation power was 20 mW @532 nm using a 100x, NA=0.9 objective. Fig. 1a was obtained with a standard back-illuminated (BI) CCD using a 62 kHz readout amplifier and 36 ms integration time/spectrum. With a little imagination, the scratch in the center of the image is just visible, but the S/N ratio is much smaller than 1.
Fig. 1b shows the same part of the sample imaged with an EMCCD with a gain of about 250. The image shows nearly the same S/N, but now the integration time was only 3.6ms, 10 times faster than in image 1a. The complete image acquisition took 25 minutes for image 1a, but only 3.4 minutes for image 1b. Fig. 1c was taken with the EMCCD, but now with the same integration time as in Fig. 1a. One can clearly see the scratch, but also the contamination in the form of a needle-like structure across the PMMA and glass surface which will be discussed later. Fig. 1d shows a sketch of the sample.
For the next images, the sample was turned upside down and an oil immersion objective with NA=1.4 was used. Integration time was 7ms/spectrum resulting in a total acquisition time of 5.4 min (including 0.3s/line for the back-scan). Fig. 2 shows 12 images acquired under the same conditions with different gain settings from 16 x to 1,000 x. Again, the signal around the CH2 stretching band was integrated to obtain the images. As one can see, the S/N ratio strongly increases up to a gain setting of about 200 x. Above this, no further improvement in S/N is visible in the images.
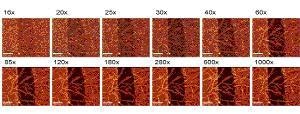
Figure 2. Comparison of confocal Raman images acquired with different settings of the EMCCD gain.
In Fig. 3, the S/N ratio of the signal from the CH2 stretching band of the PMMA is plotted against the EMCCD gain. The standard deviation of the signal was taken as noise. As one can see, the signal increases up to a gain of 300x, which appears to be the optimum setting. Above this value, the S/N value slightly decreases again. Using the appropriate gain factor, the overall improvement is more than a factor of 5.
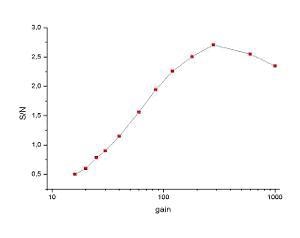
Figure 3. S/N ratio of the signal from the CH2 stretching band of PMMA plotted against the EMCCD gain.
The Identification of Contaminants
Due to the limited confocal depth resolution, none of the spectra obtained was a pure PMMA spectrum or a pure spectrum of the contamination layer. However, by averaging all spectra acquired in the area of the scratch with no contamination present, a pure glass spectrum was obtained.
By subsequent subtraction of the glass spectrum from the PMMA spectrum as well as from the spectrum of the contamination, pure PMMA and contamination spectra could be calculated. These spectra were taken for a basis analysis, in which each measured spectrum is fitted as a linear combination of basic spectra. Using this technique, three images with the distribution of the three components (glass, PMMA and contamination) could be obtained which were color-coded (blue=glass, red=PMMA and green=contamination) to visualize their distribution (Fig. 4).

Figure 4. Color-coded confocal Raman image of a 7.1 nm PMMA layer (red) and a 4.2 nm contamination layer (green) on glass (blue). 200 x 200 spectra, 7 ms integration time/spectrum. Total acquisition time 5.4 minutes.
Fig. 5 shows the spectra of the different components. For better comparison, they are displayed with identical maximum intensities. The PMMA spectrum is amplified about 20 times and the contamination spectrum about 15 times with respect to the glass spectrum.
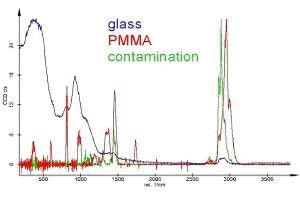
Figure 5. Raman spectra as calculated from the Raman measurement in Fig. 4, displayed with identical maximum intensities. The scale is only correct for PMMA. The PMMA spectrum is amplified about 20 times and the contamination spectrum about 15 times with respect to the glass spectrum.
From this, the green spectrum (contamination) could be easily identified as an alkane. The sample was prepared for the AFM thickness investigation several weeks before the Raman measurement and stored in a polystyrene (PS) container. These PS containers are produced by injection molding and alkane is used to coat the mold for better separation. As the sample was stored (perhaps in a warm environment), part of the alkane evaporated and condensed on the sample, which explains the needle-like structure and the fact that the coating also covers the scratch.
The scale in Fig. 5 is correct for PMMA and shows a maximum of only 28 counts. The signal averaged over the complete CH2 stretching regime (about 330 / cm or 150 pixels) is 1965 counts. The EM gain for this measurement was about 600 x, so the 1965 counts correspond to only 99 electrons (110 photons) total and 1.4 photons maximum per CCD pixel! But how can one obtain a good Raman spectrum with so few electrons? The reason is that about 20,000 spectra were averaged to calculate the PMMA spectrum shown in Fig. 5, so the overall signal is 20,000 times greater.
However, only those spectra were taken where PMMA was present. For this, the signal per spectrum must be strong enough to show the distribution of the PMMA in the Raman image, so that one is able to select the correct spectra for the averaging. As can be seen, 1.4 photons per EMCCD pixel are more than enough to visualize the distribution of the PMMA layer in this example and to choose the right spectra for the averaging process.
The result would have been even more impressive if a substrate with no background signal in the CH2 stretching regime would have been used. Fig. 6 shows the three spectra of glass, alkane and PMMA with identical intensity scale.
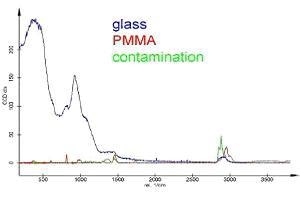
Figure 6. Same spectra as in Fig. 5 but with correct scale.
As one can see, the glass substrate used has a small Raman peak with about half of the signal of PMMA and about one third of the alkane signal in exactly this area. It is obvious that the confocality of the Raman system is crucial for the detectibility of thin layers. Even with the best confocal setup, the information depth is at least 500 nm which means that 500 nm of glass contribute to the Raman signal. As the Raman signal is proportional to the amount of material, a standard (non-confocal) setup would have collected a glass signal more than 300 times higher (170 µm cover glass thickness), making the detection of the thin coating layers impossible, even with much longer integration times.
Summary
It was demonstrated that the use of an EMCCD camera can greatly increase detection efficiency and speed, especially for the short integration times necessary with a confocal Raman microscope. The distribution of a 7.1 nm PMMA as well as a 4.2 nm alkane layer on a glass substrate could be easily detected and identified with an integration time of only 7 ms per spectrum, which reduced the overall acquisition time to 5.4 minutes for a 200 x 200 (= 40,000) spectra confocal Raman image.
For very small signals that are dominated by the CCD's readout noise, the use of an EMCCD can improve the S/N ratio by a factor of 5 - 10 compared to the best available standard CCD's, while for larger signals the electron multiplying circuit can simply be switched off and all properties of a standard (back-illuminated) CCD are maintained.

This information has been sourced, reviewed and adapted from materials provided by WITec GmbH.
For more information on this source, please visit WITec GmbH.