As the power of laboratory lasers increases, aspheric lenses and mirrors have been pushed to deliver extremely high intensities.
Around the world, nuclear research laser facilities are increasingly using powerful, amplified, ultrashort-duration pulses of coherent light in order to deliver massive energy densities at a given target. Synchronizing the delivery of these high-power pulses creates extreme conditions, in which scientists can carry out state-of-the-art nuclear research.
It also allows research into conditions that exist only in distant and exotic environments, for example, the core of our sun and beyond. Facilities such as these also provide opportunities for researchers to advance knowledge in fields such as materials science, astrophysics and particle and nuclear physics. The resulting applications range from medicine to nuclear energy.
The National Ignition Facility (NIF) at Lawrence Livermore National Laboratory in the U.S. was commissioned and constructed 10 years ago. Harnessing nuclear energy through a self-sustaining fusion reaction which would help to address the global energy crisis, however, this has still not been attained. Undoubtedly however, NIF and other laser facilities worldwide have allowed scientists to undertake ground-breaking research. This has expanded understanding of what is essential to achieve laser-induced fusion in the future.
Laser technology achievements have been remarkable. However, these advancements could not have happened if there had not also been equal progression in the design and manufacture of optics, both transmissive and reflective. One of the greatest determinants of delivered beam quality is the quality of the optics.
High-Power Laser Systems
Typically, a nuclear research laser system is composed of a series of beamlines. Through these, beams propagate and undergo expansion, power amplification, and then spatial filtering before ending at the focusing units. Focusing units are found adjacent to the vacuum chamber, which contains the diagnostic instruments and target assembly.
Since the target assembly contains the fuel capsule responsible for initiating the nuclear reaction, it is a critical component. The assembly is made up of a cylindrical cell, known as the hohlraum, a spherical fuel capsule which contains the chosen fuel, and the fuel itself.
Often, beam propagation and expansion is achieved with a series of telescopic optics. The power amplification on the other hand is typically achieved with a stack of neodymium-doped phosphate glass slabs along with a variety of powerful flashlamps. The neodymium atoms are excited to a higher energy state by the flashlamps. This means that when a low-energy laser pulse, from the injection laser system, passes though the slabs, the excess energy stored in the neodymium atoms is released into the laser pulse. This energy is released in the form of highly coherent light, of a specific wavelength.
As each beam travels back and forth through the same sets of optics and glass slabs, the pulse power amplification is repeated multiple times. This is known as a multipass scheme. By using separate, though identical, beam propagation subsystems dedicated to each beam, all beamlines undergo amplification in parallel.
The goal is to deliver a densely focused spot of coherent light inside the vacuum chamber where the fuel capsule is, from each beamline simultaneously. The simultaneous, temporally, and spatially coincident arrival of all the generated spots, at very high precision, is incredibly important. It is this precise coincidence of the densely focused spots that means that symmetrical forces can be applied to the fuel capsule. It also means that maximum energy density can be delivered to the target. Both of these things are essential requirements for meeting the conditions that would initiate a fusion reaction.
Neodymium glass lasers from NIF generate light at 1053 nm (1 ω) in the NIR region. However, prior to focusing it on the target, the laser light is converted to its third harmonic 351 nm (3 ω). The frequency conversion is achieved using two nonlinear crystal plates made of potassium dihydrogen phosphate (KDP). The conversion is necessary since inertial confinement fusion targets absorb UV much more efficiently compared to longer wavelengths. Performance is also better at shorter wavelengths.
After the UV rays have been efficiently absorbed, the temperature around the fuel capsule is increased immensely by the generation of secondary x-rays. This extreme local environment initially causes a temperature increase and ablation on the surface of the fuel capsule. The shockwaves that are produced during the ablation make the capsule collapse in a rapid implosion. This rapid implosion compresses the DT (deuterium and tritium) fuel to extreme densities and heats it to intense temperatures.
As previously discussed, the distribution of forces within the target, although not exclusively dependent, relies heavily on the synchronization and precision of the delivered beams. A successful beam delivery of a highly dense energy is likely to cause a symmetrical implosion and compression and so raise the temperatures to a sufficient level (in excess of 100 million degrees). Under these temperatures, the fusion reaction equals or exceeds the laser energy deposited in the target. This is a condition known as Lawson criterion, or ignition.
However, achieving the temperature and pressure necessary to initiate a self-sustained fusion reaction through the precise application of symmetric shockwaves remains technically elusive. A technique known as “fast ignition” relaxes some of these constraints.
This is done by providing a very short (picosecond or femtosecond) burst of energy directly at one side of the core fuel once the explosion reaches maximum density. Fast ignition is currently being explored as a viable option that could improve the performance of inertial confinement fusion reactions.
High-Power Facilities
The proposed European High power laser Energy facility (HiPER) is one example of an attempt to use fast ignition to initiate self-sustaining fusion. It is expected that this facility will use less energy during operation than NIF, whilst at the same time producing significantly higher fusion gains (a thermonuclear gain of 100). However, until funding is secured, the roadmap toward commissioning remains uncertain.
The ELI Beamlines Laser Research Centre in the Czech Republic uses various complete laser systems. These include the L1 Alegra, L2 Amos, L3 HAPLS and the L4-Aton with ultrashort laser pulses. These systems include options of high power and high repetition rate as well as up to a very high power, single shot (10-PW) configuration.
The ELI project has numerous objectives. One of the main objectives is to produce particles and radiation from ultrarelativistic and relativistic interactions, using the single-shot, ultrashort high-peak-power laser options. This will allow scientists to examine how matter behaves at the ultrarelativistic regime, this results in a state of matter known as quantum plasma.
It is estimated that the 10-PW laser at the facility will provide basic scientific research projects with a focused intensity of up to 1024 W/cm2, at an increased dose rate. Rather than pursuing advancements in nuclear energy, the ultrashort pulse sources are designed to serve the needs of fundamental research.
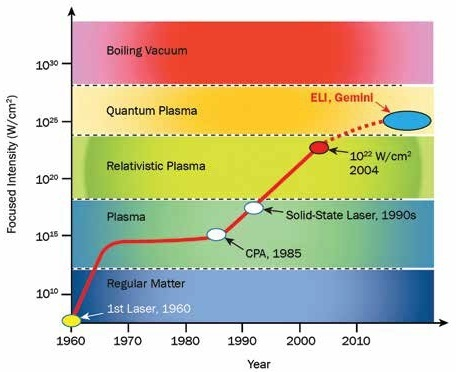
Figure 1. A history of laser intensity, with various laser-matter interaction periods. Image Credit: Optical Surfaces
Studies were conducted in the relativistic and subrelativistic regimes over the past 20 years1,2,3. Recent efforts include ELI4 and the Gemini Laser Facility, and potentially in the future, HiPER. The aim of these efforts is to address the ultrarelativistic regime, or the quantum state, with expected focused intensities of > 1023 W/cm2 (figure 1). The amplification of ultrashort pulses to the petawatt level are enabled by technological advancements, such as the CPA (chirped pulse amplification) which was developed in 1985. In the 1990s, the development of solid-state lasers allowed the generation of ultrafast picosecond and femtosecond pulses. These advances were key landmarks in the pursuit of generating quantum plasma and relativistic states.
In the CPA technique, a pair of gratings is used to stretch out an ultrashort laser pulse in time before it is introduced to the grain medium. The gratings are arranged so that the varying frequency components of the laser pulse travel over unequal paths. This process is known as pulse stretching. Then, the intensity of individual parts of the spectrum can be reduced and these are spread to levels sufficient to undergo amplification. This is done without damaging the grain medium by overloading it while the pulse passes through.
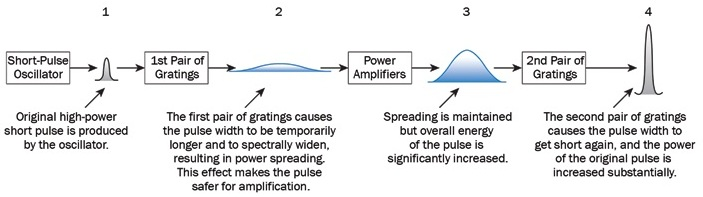
Figure 2. Schematic of the CPA technique and amplification stages. Image Credit: Optical Surfaces
Lastly, the stretched, amplified laser pulse is recompressed into its original pulse width. This is achieved by reversing the process of stretching. This system achieves peak powers that are orders of magnitude greater than could be generated using laser systems before CPA (Figure 2).
Focusing Optics
One of the most important roles in the successful delivery of high-uniformity, high-density distribution of energy to the target, which is a critical aspect of all laser-based nuclear research projects, is the focusing optics. A successful delivery can be achieved with either aspheric reflective mirrors, for example off-axis parabolas which often have a large off-axis angle, or with transmissive aspheric focusing lenses, or possibly with long-short pulse combinations of the two5. This is dependent on the particular operational needs and design in each laser facility.
Since very short pulses tend to spread significantly as they transmit through glass, lasers that produce ultrashort pulses need reflective optics. Longer pulses however, do not show significant spreading and so using transmissive elements, such as lenses, is a less viable option.
M. Rosete-Aguilar and colleagues have extensively addressed the effects of optical materials on temporal spreading of an optical pulse whilst traveling though materials such as these6. This study looked at glasses with different chromatic dispersion characteristics and analyzed their spreading as a function of wavelength for different pulse widths.
The effect of glasses on pulse temporal widening is significantly more severe on ultrashort compared to longer pulses (e.g., pulse lengths >> 100 fs). This phenomenon was confirmed by this study. Additionally, the effects appear to be significantly more pronounced as the wavelengths approach UV (such as 351 nm). This behavior is demonstrable in all types of glasses to varying degrees. Of the glasses studies, fused silica appears to exhibit the best behavior6.
Taking the above into consideration, deciding whether to use a transmissive or optical component depends heavily on whether the experiments use ultrashort pulses or not. For example, a reflective solution should be chosen in the case of ELI because a single ultrashort pulse is used. However, in other cases, such as NIF, a transmissive solution is preferable because multiple longer pulses are used.
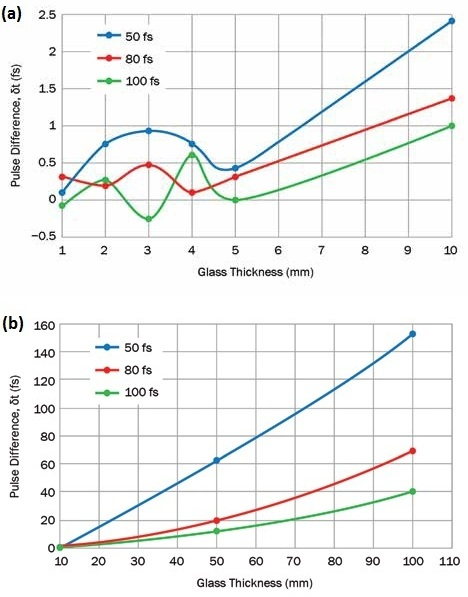
Figure 3. Pulse spreading through 1- to 10-mm-thick blocks (a) and through 10- to 100-mm-thick blocks (b). Image Credit: Optical Surfaces
Data processed from Rosete-Aguilar and colleagues shows the added spread on a pulse as the beam propagates through glasses of varying thickness. Figure 3 demonstrates the unsuitability of lenses for ultrashort pulses for the case of fused silica, with pulses ranging from 50 to 100 fs and a wavelength of 800 nm. For thin blocks of glass (e.g., 10 mm thick), this result becomes negligible. This suggests that using thinner optics, including optical windows, may be acceptable even in ultrashort pulses.
However, the need to deliver an in-phase, free-of-aberration, high-precision and highly dense spot of light at the focal plane means that the user has to adopt optics with short focal lengths and larger apertures. These requirements can only be satisfied using highly aspheric mirrors and lenses, which are naturally free of spherical aberrations.
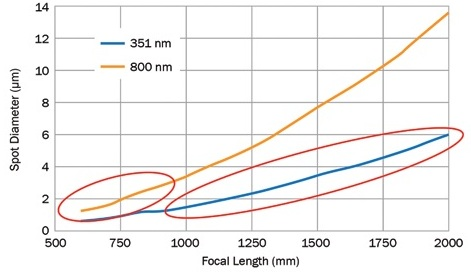
Figure 4. The relationship between focal length and focused spot diameter for a given input beam diameter. The blue line represents a scenario similar to the NIF’s operational needs, where multiple short-pulse beams at 351 nm converge toward the target. The orange line represents a scenario similar to ELI’s, where a single high-peak-power ultrashort shot is delivered at 800 nm. Image Credit: Optical Surfaces
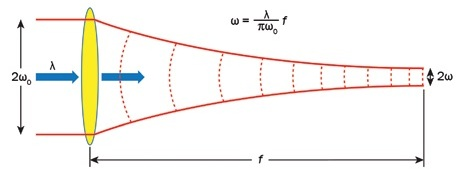
Figure 5. Gaussian beam propagation theory applied to a beam going through a focusing element. Image Credit: Optical Surfaces
Selecting the correct optics can assist in delivering a targeted spot of light, only a few microns in diameter, at the target (Figure 4). The calculations assume perfect optics, a perfect Gaussian beam of 300 mm diameter aperture, and also Gaussian beam propagation theory (Figure 5). An aspheric focusing lens with a focal length of 1 to 3 m can be considered to be an appropriate choice in nuclear laser facilities.
This is dependent on the number of beamlines used, the diameter of the chamber, and other design parameters. However, the most appropriate solution is an off-axis parabolic mirror with a very short focus length. A number of additional reasons not addressed here in detail also make this the most appropriate choice.
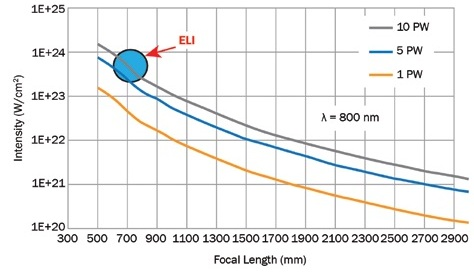
Figure 6. Graph illustrating the need to resort to very high-power petawatt lasers and a very short focal length mirror to generate ultrarelativistic plasma (ELI). Image Credit: Optical Surfaces
Using the example of ELI, it was possible to further extrapolate the data to ascertain that the focal length of the off-axis parabolic mirror required to permit generation of ultrarelativistic plasma according to the designers’ aspirations, would need to lie within the region of 700 mm (Figures 6 and 1). This objective relates to the goal of achieving focusing intensities which aim to exceed the 1023 W/cm2 barrier.
References
- G.A. Mourou et al. (2007). Relativistic laser-matter interaction: from attosecond pulse generation to fast ignition. Plasma Phys Control Fusion, Vol. 49, p. B667.
- T.Z. Esirkepov et al. (2012). Fundamental physics and relativistic laboratory astro- physics with extreme power lasers. EAS Publ Ser, Vol. 58, pp. 7-22.
- J. Yee and S.T. Cundiff (2005). Femtosecond Optical Frequency Comb Technology: Principle, Operation and Applications. Boston: Springer Science + Business Media Inc., p. 55.
- G.A. Mourou et al. (2011). ELI-Extreme Light Infrastructure — Whitebook: Science and Technology with Ultra-Intense Lasers. ELI PP Publications.
- N. Hopps et al. (2013). Overview of laser systems for the Orion facility at the AWE. Appl Optics, Vol. 52, No. 15, pp. 3597-3607. 6. M. Rosete-Aguilar et al. (2008). Calculation of temporal spreading of ultrashort pulses propagating through optical glasses. Rev Mex Fis E, Vol. 54, No. 2, pp. 141-148.
Acknowledgments
Produced from materials originally authored by Aris Kouris from Optical Surfaces Ltd, originally published in Photonics Spectra (September and October 2019 issues).

This information has been sourced, reviewed and adapted from materials provided by Optical Surfaces Ltd.
For more information on this source, please visit Optical Surfaces Ltd.